题目内容
1.△ABC的三个内角A,B,C的对边分别为a,b,c,且asinB=bcosA,则$2sinB-\sqrt{2}cosC$的最大值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
分析 利用正弦定理以及两角和的正弦函数求出A的值,通过内角和化简所求表达式为B的三角函数,然后求出表达式的最大值.
解答 解:由asinB=bcosA以及正弦定理可知sinAsinB=sinBcosA,⇒A=$\frac{π}{4}$,
∴$2sinB-\sqrt{2}cosC$
=2sinB-$\sqrt{2}$cos($\frac{3π}{4}$-B)
=2sinB-$\sqrt{2}$(cos$\frac{3π}{4}$cosB+sin$\frac{3π}{4}$sinB)
=2sinB+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$cosB-$\sqrt{2}$×$\frac{\sqrt{2}}{2}$sinB
=2sinB+cosB-sinB
=$\sqrt{2}$sin($\frac{π}{4}$+B).
∴$2sinB-\sqrt{2}cosC$的最大值为$\sqrt{2}$.
故选:A.
点评 本题考查正弦定理的应用,三角函数中的恒等变换的应用,考查计算能力.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案
相关题目
9.已知a,b,c满足a>b>c,ac<0,则下列不等关系中正确的是( )
| A. | cb2<ab2 | B. | ab<ac | C. | c(a-c)>0 | D. | a+ac>b+ac |
6.下列哪个函数是周期为π的偶函数( )
| A. | y=sin2x | B. | y=|sin2x| | C. | y=cos2x | D. | y=|cos2x| |
13.运行如图所示的流程图,则输出的结果S是( )
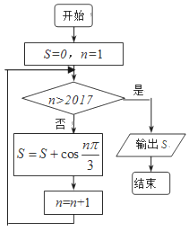

| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | -1 | D. | 1 |
11.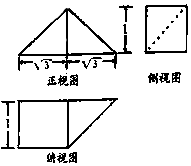 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )
 《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,已知某“堑堵”与某“阳马”组合而成的几何体的三视图如图所示,则该几何体的表面积( )| A. | $4+3\sqrt{3}$ | B. | $3+3\sqrt{3}$ | C. | $4+2\sqrt{3}$ | D. | $3+4\sqrt{3}$ |
