题目内容
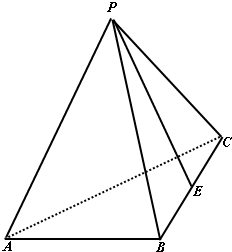
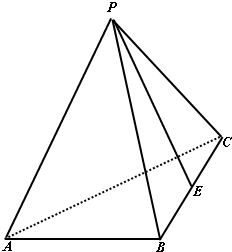 在三棱锥P-ABC内,已知PA=PC=AC=
在三棱锥P-ABC内,已知PA=PC=AC= ,AB=BC=1,面PAC⊥面ABC,E是BC的中点.
,AB=BC=1,面PAC⊥面ABC,E是BC的中点.
(1)求直线PE与AC所成角的余弦值;
(2)求直线PB与平面ABC所成的角的正弦值;
(3)求点C到平面PAB的距离.
 解:(1)分别取AB,AC的中点F,H,连接PH,HF,HE,EF
解:(1)分别取AB,AC的中点F,H,连接PH,HF,HE,EF由于E、F分别是BC、AB的中点,故EF是△ABC的中位线,则有EF∥AC,
故∠PEF是异面直线PE与AC所成的角或补角
在△PEF中,PE=PF=
 ,EF=
,EF=
故cos∠PEF=
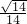
(2)由于PA=PC,H是AC的中点,
有PH⊥AC
又由面PAC⊥面ABC
面PAC∩面ABC=AC
有PH⊥面ABC
故∠PBH是直线PB与平面ABC所成的角
在△PBH中,PH=
 ,PH=
,PH=
∴tan∠PBH=
 =
=
故sin∠PBH=

(3)∵VP-ABC=VC-PAB=
 S△ABC•PH=
S△ABC•PH= •
• ×1×1×
×1×1× =
=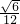
又由三角形PAB的面积S△PAB=

∴点C到平面PAB的距离h=
 =
=
分析:(1)分别取AB,AC的中点F,H,连接PH,HF,HE,EF,根据三角形中位线定理可得EF∥AC,即∠PEF是异面直线PE与AC所成的角或补角,解△PEF即可得到答案.
(2)由PA=PC,H是AC的中点,结合等腰三角形“三线合一”的性质,我们易得PH⊥AC,再由面面垂直的性质,得到PH⊥面ABC,故∠PBH是直线PB与平面ABC所成的角,解△PBH即可得到直线PB与平面ABC所成的角的正弦值;
(3)利用等体集法,根据VP-ABC=VC-PAB,分别求出棱锥P-ABC的体积及底面三角形PAB的面积,进而得到点C到平面PAB的距离.
点评:本题考查的知识点是点、面间的距离计算,异面直线及其所成的角,直线与平面所成的角,其中(1)的关键是确定∠PEF是异面直线PE与AC所成的角或补角,(2)的关键是证得∠PBH是直线PB与平面ABC所成的角,(3)是的等体积法是求点到平面距离的常用方法.

练习册系列答案
相关题目
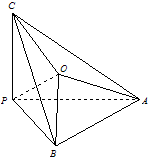 如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPA=45°,∠OPB=60°,则∠OPC的度数为( )
如图,在三棱锥P-ABC中,∠APB=∠BPC=∠APC=90°,O在△ABC内,∠OPA=45°,∠OPB=60°,则∠OPC的度数为( )| A、30° | B、45° | C、60° | D、75° |
 在三棱锥P-ABC内,已知PA=PC=AC=
在三棱锥P-ABC内,已知PA=PC=AC=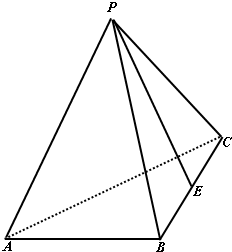
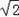 ,AB=BC=1,面PAC⊥面ABC,E是BC的中点.
,AB=BC=1,面PAC⊥面ABC,E是BC的中点.