Question

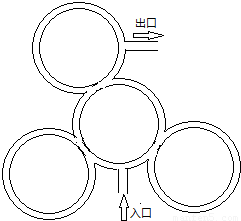
一人在如图所示景点中的圆环道路上散步．他在交叉路口偏左走的概率为，偏右走的概率为（出口处不算交叉路口）．
（Ⅰ）求这个人路过的交叉路口数最少且走出景点的概率；
（Ⅱ）这个人有3天散步路过的交叉路口都最少，ξ表示这个人这3天中相同的线路次数，求ξ的分布列和数学期Eξ．

Answer 1

【答案】分析：（Ⅰ）由图可知，此人走出景点遇到的最少交叉路口数为4，求出相应的概率，利用互斥事件的概率公式，即可求这个人路过的交叉路口数最少且走出景点的概率；
（Ⅱ）确定ξ的取值，求出相应的概率，即可求分布列和数学期Eξ．
解答：解：（Ⅰ）由图可知，此人走出景点遇到的最少交叉路口数为4，共分：①入口⇒向左⇒向左⇒向左⇒向左⇒出口，②入口⇒向左⇒向右⇒向右⇒向左⇒出口，③入口⇒向右⇒向左⇒向左⇒向右⇒出口，④入口⇒向右⇒向右⇒向右⇒向右⇒出口，一共4条线路．设此人选择这4条线路分别为事件A、B、C、D，设“此人遇到的交叉路口数为4”为事件E，则A、B、C、D互斥，且E=A+B+C+D
由题意，P（A）=P（B）=P（C）=，
∴．
答：这个人路过的交叉路口数最少且走出景点的概率为．…6分
（Ⅱ）由题意，ξ=0，1，2，…7分
，，，
∴ξ的分布列为

ξ		1	2
p

∴．…13分．
点评：本题考查概率的计算，考查离散型随机变量的分布列与数学期望，考查学生的计算能力，属于中档题．