题目内容
(本小题12分)
设函数![]()
(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,设
时,设![]() 的最小值为
的最小值为![]() 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
(Ⅰ)解:![]() , ┄┄┄┄┄┄1分
, ┄┄┄┄┄┄1分
当![]() 时,
时,![]() ,
,
所以函数![]() 的减区间为
的减区间为![]() ,无增区间;
,无增区间;
当![]() 时,
时,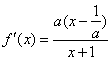 ,
,
若![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
所以函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ;
;
若![]() ,此时
,此时![]() ,所以
,所以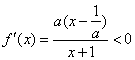 ,
,
所以函数![]() 的减区间为
的减区间为![]() ,无增区间;
,无增区间;
综上,当![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,无增区间,
,无增区间,
当![]() 时,函数
时,函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .┄6分
.┄6分
(Ⅱ)解:由(Ⅰ)得,![]() , ┄┄┄┄┄┄7分
, ┄┄┄┄┄┄7分
因为![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() 恒成立,
恒成立,
由于![]() ,
,
当![]() 时,
时,![]() ,故函数
,故函数![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() 成立; ┄┄┄┄┄┄10分
成立; ┄┄┄┄┄┄10分
当![]() 时,若
时,若![]() 得
得![]() ,
,
故函数![]() 在
在![]() 上是增函数,
上是增函数,
即对![]() ,
,![]() ,与题意不符;
,与题意不符;
综上,![]() 为所求. ┄┄┄┄┄┄12分
为所求. ┄┄┄┄┄┄12分

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 是定义在
是定义在 上的偶函数,已知
上的偶函数,已知 时,
时, .
.
 的圆柱.
的圆柱.
 的方程
的方程
 .
.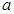 的取值范围.
的取值范围.