题目内容
已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则sin(
+θ)=
| π |
| 2 |
±
| ||
| 5 |
±
.
| ||
| 5 |
分析:由题意可得tanθ=2,即
=2,再由 sin2θ+cos2θ=1 可得 cos2θ=
,从而得到 sin(
+θ)=cosθ 的值.
| sinθ |
| cosθ |
| 1 |
| 5 |
| π |
| 2 |
解答:解:∵角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则有tanθ=2,即
=2.
再由 sin2θ+cos2θ=1 可得 cos2θ=
,∴sin(
+θ)=cosθ=±
,
故答案为 ±
.
| sinθ |
| cosθ |
再由 sin2θ+cos2θ=1 可得 cos2θ=
| 1 |
| 5 |
| π |
| 2 |
| ||
| 5 |
故答案为 ±
| ||
| 5 |
点评:本题主要考查任意角的三角函数的定义,同角三角函数的基本关系的应用,属于中档题.

练习册系列答案
相关题目
 和
和 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴的正半轴重合,角
轴的正半轴重合,角 上,角
上,角 的对称直线m上,则
的对称直线m上,则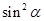 =
=  ),且2α∈[0,2π),则tanα等于( )
),且2α∈[0,2π),则tanα等于( )