题目内容
已知函数f（x）=x-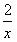
+a（2-lnx），a＞0，讨论f（x）的单调性。
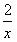+a（2-lnx），a＞0，讨论f（x）的单调性。 解：f（x）的定义域是(0，+∞)，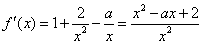
，
设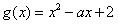
，二次方程g（x）=0的判别式
，
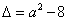①当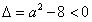
，即
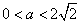时，对一切x＞0都有f′（x）＞0，此时f（x）在(0，+∞)上是增函数；
②当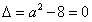
，即
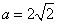时，仅对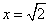
有f′（x）=0，对其余的x＞0都有f′（x）＞0，此时f（x）在(0，+∞)上也是增函数；
③当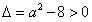
，即
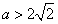时，
方程g（x）=0有两个不同的实根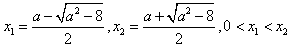
，
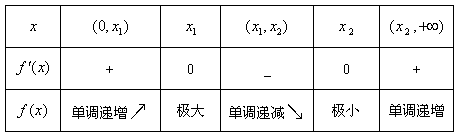
此时f（x）在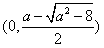
上单调递增， 在
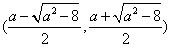上单调递减， 在
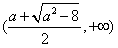上单调递增。
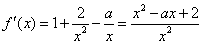，设
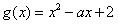，二次方程g（x）=0的判别式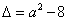，①当
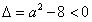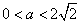，即时，对一切x＞0都有f′（x）＞0，此时f（x）在(0，+∞)上是增函数；②当
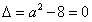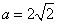，即时，仅对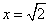有f′（x）=0，对其余的x＞0都有f′（x）＞0，此时f（x）在(0，+∞)上也是增函数；③当
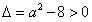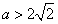，即时，方程g（x）=0有两个不同的实根
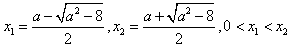， 此时f（x）在
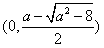上单调递增， 在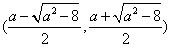上单调递减， 在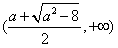上单调递增。
练习册系列答案
口算题天天练系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|