题目内容
函数f(x)=m-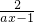 为奇函数,则m=________.
为奇函数,则m=________.
-2
分析:由奇函数定义得,对定义域内的所有x,都有f(-x)=-f(x),根据该等式恒成立可求得m值.
解答:因为f(x)为奇函数,所以对定义域内的所有x,都有f(-x)=-f(x),
即m- =-(m-
=-(m-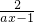 ),
),
2m=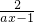 -
- =
= ,
,
a2x2= ,
,
所以a=0,m+2=0,解得m=-2.
故答案为:-2.
点评:本题考查奇函数的性质,属基础题,定义是解决该类问题的基本方法.
分析:由奇函数定义得,对定义域内的所有x,都有f(-x)=-f(x),根据该等式恒成立可求得m值.
解答:因为f(x)为奇函数,所以对定义域内的所有x,都有f(-x)=-f(x),
即m-
 =-(m-
=-(m-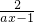 ),
),2m=
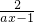 -
- =
= ,
,a2x2=
 ,
,所以a=0,m+2=0,解得m=-2.
故答案为:-2.
点评:本题考查奇函数的性质,属基础题,定义是解决该类问题的基本方法.

练习册系列答案
相关题目