题目内容
已知函数 ,在定义域
,在定义域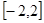 上表示的曲线过原点,且在
上表示的曲线过原点,且在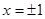 处的切线斜率均为
处的切线斜率均为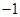 .有以下命题:
.有以下命题:
① 是奇函数;②若
是奇函数;②若 在
在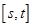 内递减,则
内递减,则 的最大值为4;③
的最大值为4;③ 的最大值为
的最大值为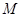 ,最小值为
,最小值为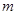 ,则
,则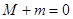 ; ④若对
; ④若对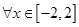 ,
,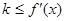 恒成立,则
恒成立,则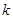 的最大值为2.其中正确命题的序号为
的最大值为2.其中正确命题的序号为
①③
解析试题分析:因为函数 ,在定义域
,在定义域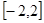 上表示的曲线过原点,
上表示的曲线过原点, ,
,
又 ,且在
,且在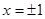 处的切线斜率均为
处的切线斜率均为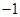 ,
,
 ,
, .
.
① ,
, 是奇函数.①正确
是奇函数.①正确
②由 ,
, 在
在 内单调递减,若
内单调递减,若 在
在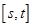 内递减,则
内递减,则 的最大值为
的最大值为 .②错误;
.②错误;
③由奇函数的关于原点对称可知,最大值与最小值互为相反数, 的最大值为
的最大值为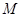 ,最小值为
,最小值为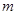 ,则
,则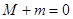 ;③正确;
;③正确;
④对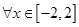 ,由于
,由于 ,则
,则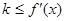 恒成立,则
恒成立,则 k≤-4,则
k≤-4,则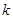 的最大值为-4.④错误.
的最大值为-4.④错误.
考点:函数的导数的几何意义的应用,函数的奇偶性及单调性.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 .若存在实数
.若存在实数 ,
, ,使得
,使得 的解集恰为
的解集恰为 ,则
,则 的取值范围是 .
的取值范围是 . 是函数
是函数 的一个零点,则函数
的一个零点,则函数 在区间
在区间 内所有极值点之和为
内所有极值点之和为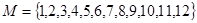 ,以下命题正确的序号是 .
,以下命题正确的序号是 .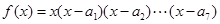 ,其中
,其中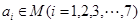 ,那么
,那么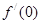 的最大值为
的最大值为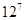 。
。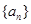 满足首项
满足首项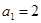 ,
,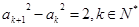 ,当
,当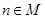 且
且 最大时,数列
最大时,数列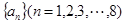 满足
满足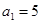 ,
,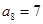 ,
,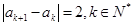 ,如果数列
,如果数列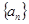 一共有33个。
一共有33个。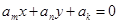 ,其中
,其中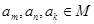 ,而且
,而且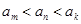 ,则一共可以得到不同的直线196条。
,则一共可以得到不同的直线196条。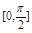 上的值域为_____________;
上的值域为_____________; 处的切线方程为 。
处的切线方程为 。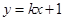 与曲线
与曲线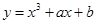 切于点
切于点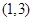 ,则
,则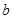 的值为__________.
的值为__________. 的导函数为
的导函数为 ,则
,则  的值为 .
的值为 .