Question

已知正△ABC的边长为a,在平面上求一点P,使|PA|²+|PB|²+|PC|²最小,并求出此最小值.

Answer 1

解:如图,以BC所在直线为x轴,BC的垂直平分线为y轴建立直角坐标系,则

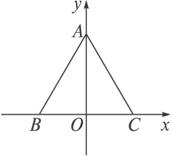
A(0,a),B(,0),C(,0).

设P(x,y),

则|PA|²+|PB|²+|PC|²

=x²+(y-a)²+(x+)²+y²+(x-)²+y²

=3x²+3y²-ay+

=3x²+3(y-a)²+a²≥a²,

当且仅当x=0,y=a时,等号成立,

∴所求最小值为a²,此时P点坐标为P(0,a),是正△ABC的中心.