Question

我们把形如y=

b

|x|-a

（a＞0，b＞0）的函数称为“莫言函数”，并把其与y轴的交点关于原点的对称点称为“莫言点”，以“莫言点”为圆心凡是与“莫言函数”有公共点的圆，皆称之为“莫言圆”，则当a=1，b=1时，
（1）莫言函数的单调增区间为：

 

（2）所有的“莫言圆”中，面积的最小值为

 

．

Answer 1

考点：函数与方程的综合运用

专题：函数的性质及应用

分析：（1）根据已知中关于“莫言函数”，“莫言点”，“莫言圆”的定义，利用a=1，b=1，我们易求出“莫言点”坐标，画出“莫言函数”的图象，进而得到函数的单调增区间．
（2）设出“莫言圆”的方程，根据两点的距离公式求出圆心到“莫言函数”图象上点的最小距离，即可得到结论．

解答： 解：当a=1且b=1时，函数“莫言函数”为y=

1

|x|-1

，
其图象由函数y=

1

x

的图象向右平移一个单位，再做横向对折变换得到，
故图象如下图所示：

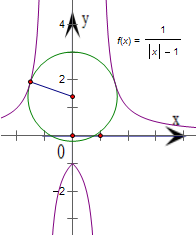
由图可得，莫言函数的单调增区间为：（-∞，-1），（-1，0]；
（2）由（1）中函数图象与y轴交于（0，-1）点，
则“莫言点”坐标为（0，1）．
令“莫言圆”的标准方程为x²+（y-1）²=r²，
令“莫言圆”与函数y=

1

|x|-1

图象的左右两支相切，
则可得切点坐标为（

1+ 5

2

，

1+ 5

2

）和（-

1+ 5

2

，

1+ 5

2

），
此时“莫言圆”的半径r=

( 1+ 5 2 )2+(1- 1+ 5 2 )2

=

3

；
令“莫言圆”与函数y=

1

|x|-1

图象的下支相切，此时切点坐标为（0，-1）．
此时“莫言圆”的半径r=2；
故所有的“莫言圆”中，面积的最小值为3π．
故答案为：（-∞，-1），（-1，0]，3π

点评：本题给出“莫言函数”、“莫言点”、“莫言圆”的定义，求圆的最小面积．着重考查了函数的图象、圆的方程、两点的距离公式与圆面积求法等知识，属于中档题．