题目内容
已知圆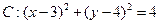 和直线
和直线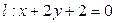 ,直线
,直线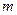 ,
,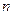 都经过圆C外
都经过圆C外
定点A(1,0).
(Ⅰ)若直线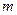 与圆C相切,求直线
与圆C相切,求直线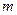 的方程;
的方程;
(Ⅱ)若直线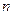 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与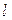 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,
求证: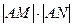 为定值.
为定值.
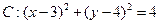 和直线
和直线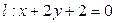 ,直线
,直线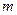 ,
,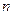 都经过圆C外
都经过圆C外定点A(1,0).
(Ⅰ)若直线
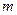 与圆C相切,求直线
与圆C相切,求直线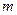 的方程;
的方程;(Ⅱ)若直线
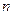 与圆C相交于P,Q两点,与
与圆C相交于P,Q两点,与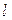 交于N点,且线段PQ的中点为M,
交于N点,且线段PQ的中点为M,求证:
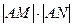 为定值.
为定值.(1) ,
, (2)6
(2)6
 ,
, (2)6
(2)6(Ⅰ)①若直线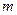 的斜率不存在,即直线是
的斜率不存在,即直线是 ,符合题意.
,符合题意.
②若直线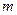 斜率存在,设直线
斜率存在,设直线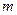 为
为 ,即
,即 .
.
由题意知,圆心(3,4)到已知直线 的距离等于半径2,
的距离等于半径2,
即: ,解之得
,解之得  .
.
所求直线方程是 ,
, .
.
(Ⅱ)解法一:直线与圆相交,斜率必定存在,且不为0,
可设直线方程为
由 得
得 .
.
再由
得 .
.
∴ 得
得 .
.
∴
 为定值
为定值
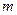 的斜率不存在,即直线是
的斜率不存在,即直线是 ,符合题意.
,符合题意. ②若直线
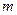 斜率存在,设直线
斜率存在,设直线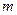 为
为 ,即
,即 .
.由题意知,圆心(3,4)到已知直线
 的距离等于半径2,
的距离等于半径2,即:
 ,解之得
,解之得  .
. 所求直线方程是
 ,
, .
.(Ⅱ)解法一:直线与圆相交,斜率必定存在,且不为0,
可设直线方程为

由
 得
得 .
.再由

得
 .
.∴
 得
得 .
. ∴

 为定值
为定值
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
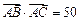 .
.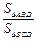 的值.
的值.
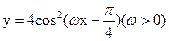 的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若
的图象与直线y=3在y轴右侧的交点按横坐标从小到大依次为P1,P2,P3,…,若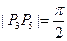 ,则
,则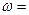 。
。 若直线
若直线 :
: 与线段PQ的延长线相交,则
与线段PQ的延长线相交,则 的取值范围是 .
的取值范围是 .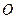 的半径为
的半径为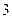 ,从圆
,从圆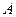 引切线
引切线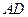 和割线
和割线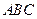 ,
,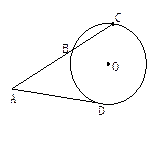

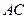 的距离为
的距离为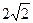 ,
,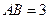 ,则切线
,则切线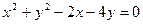 截直线
截直线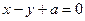 得弦长为
得弦长为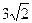 ,则a的值为(
,则a的值为(  )
)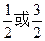
 的右焦点为
的右焦点为 ,则该双曲线的渐近线方程为 .
,则该双曲线的渐近线方程为 .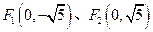 ,动点
,动点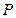 满足条件:
满足条件: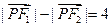 ,设点
,设点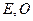 为坐标原点。
为坐标原点。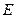 的方程;
的方程;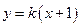 与曲线
与曲线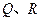 ,求
,求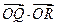 的取值范围;
的取值范围;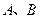 两点分别在直线
两点分别在直线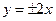 上,若
上,若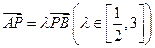 ,记
,记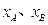 分别为
分别为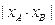 的最小值。
的最小值。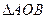 面积的最大值。
面积的最大值。