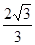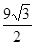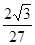题目内容
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点B恰好是抛物线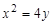 的焦点,且离心率等于
的焦点,且离心率等于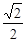 ,直线
,直线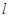 与椭圆C交于M,N两点.
与椭圆C交于M,N两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)椭圆C的右焦点F是否可以为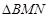 的垂心?若可以,求出直线
的垂心?若可以,求出直线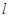 的方程;若不行,请说明理由.
的方程;若不行,请说明理由.
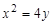 的焦点,且离心率等于
的焦点,且离心率等于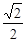 ,直线
,直线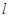 与椭圆C交于M,N两点.
与椭圆C交于M,N两点.(Ⅰ)求椭圆C的方程;
(Ⅱ)椭圆C的右焦点F是否可以为
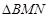 的垂心?若可以,求出直线
的垂心?若可以,求出直线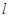 的方程;若不行,请说明理由.
的方程;若不行,请说明理由. (Ⅰ) ;(Ⅱ)
;(Ⅱ) 。
。
 ;(Ⅱ)
;(Ⅱ) 。
。试题分析:(Ⅰ)设椭圆C的方程:
 ,
,由题意知
 ,
,

∴ 椭圆C的方程为:

(Ⅱ)假设存在这样的直线
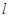 ,使得
,使得 是
是 的垂心,直线BF的斜率为
的垂心,直线BF的斜率为 ,
,从而直线
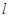 的斜率为
的斜率为 ,设直线
,设直线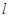 的方程为
的方程为 ,
,由

 ,设
,设
则
 ,且
,且 ,
,


 ,解得
,解得 或
或
当
 时点B为直线
时点B为直线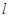 与椭圆的一个交点,不合题意舍去;
与椭圆的一个交点,不合题意舍去;当
 时,直线
时,直线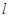 与椭圆相交两点,且满足题意;
与椭圆相交两点,且满足题意;综上可知直线
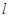 的方程为
的方程为 时,椭圆C的右焦点F是可以为
时,椭圆C的右焦点F是可以为 的垂心 。
的垂心 。点评:本题考查了椭圆方程的求法,以及存在性问题的做法,为圆锥曲线的常规题,应当掌握。考查了学生综合分析问题的能力,知识的迁移能力以及运算能力。解题时要认真审题,仔细分析。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
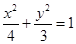 上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于
上有n个不同的点:P1 ,P2 ,…,Pn, 椭圆的右焦点为F,数列{|PnF|}是公差大于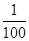 的等差数列, 则n的最大值是( )
的等差数列, 则n的最大值是( )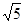 ,离心率
,离心率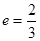 的椭圆两焦点为
的椭圆两焦点为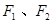 , 过
, 过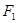 作直线交椭圆于
作直线交椭圆于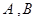 两
两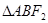 的周长为( )
的周长为( ) 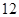
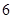
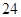
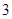
 的焦距是
的焦距是



 成等比数列,且抛物线
成等比数列,且抛物线 的顶点是
的顶点是 ,
, 等于
等于  的离心率是
的离心率是 ,其焦点为
,其焦点为 ,P是双曲线上一点,
,P是双曲线上一点, ,若
,若 的面积等于9,则
的面积等于9,则 ( )
( )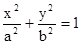 (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为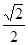 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N.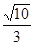 时,求k的值.
时,求k的值.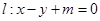 与抛物线
与抛物线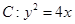 交于不同两点A、B,F为抛物线的焦点。
交于不同两点A、B,F为抛物线的焦点。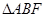 的重心G的轨迹方程;
的重心G的轨迹方程;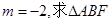 的外接圆的方程。
的外接圆的方程。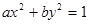 与直线
与直线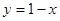 交于
交于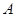
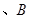 两点,过原点与线段
两点,过原点与线段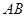 中点的直线的斜率为
中点的直线的斜率为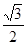 ,则
,则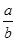 的值为 ( )
的值为 ( )