题目内容
已知函数
(Ⅰ)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=x+2垂直,求函数y=f(x)的单调区间;
(Ⅱ)若对于任意 成立,试求a的取值范围;
成立,试求a的取值范围;
(Ⅲ)记g(x)=f(x)+x-b(b∈R).当a=1时,函数g(x)在区间 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。
解:(Ⅰ)直线y=x+2的斜率为1, 函数f(x)的定义域为 
因为 ,所以
,所以 ,所以a=1
,所以a=1
所以
由 解得x>2 ; 由
解得x>2 ; 由 解得0<x<2
解得0<x<2
所以f(x)得单调增区间是 ,单调减区间是
,单调减区间是
(Ⅱ)
由 解得
解得 由
由 解得
解得
所以f(x)在区间 上单调递增,在区间
上单调递增,在区间 上单调递减
上单调递减
所以当 时,函数f(x)取得最小值
时,函数f(x)取得最小值
因为对于任意 成立,
成立,
所以 即可
即可
则 ,由
,由 解得
解得
所以a得取值范围是 xk.Com]
xk.Com]
(Ⅲ)依题意得 ,则
,则
由 解得x>1,由
解得x>1,由 解得0<x<1
解得0<x<1
所以函数g(x)在区间 上有两个零点,
上有两个零点,
所以 解得
解得
所以b得取值范围是

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
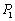 ,
,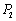 ,…,
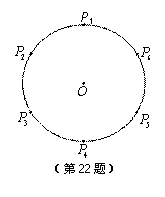
,…,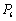 为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一
为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一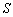 .
.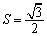 的概率;
的概率;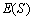 .
.
 在x=1处的切线与两坐标轴围成的三角形的面积为4,则
在x=1处的切线与两坐标轴围成的三角形的面积为4,则 = .
= . 外接圆半径等于1,其圆心
外接圆半径等于1,其圆心 满足
满足 ,则向量
,则向量 在
在 方向上的投影等于( )
方向上的投影等于( ) B.
B. C.
C. D.3
D.3 ,
, ,对于区间
,对于区间
 上的任意实数
上的任意实数 ,有如下条件:
,有如下条件:  ,其中能使
,其中能使 恒成立的条件的序号有_________。(写出你认为成立的所有条件序号)
恒成立的条件的序号有_________。(写出你认为成立的所有条件序号) 与直线
与直线 平行,则实数
平行,则实数 的取值为
的取值为 B.
B. C.
C.  D.
D.
 的离心率为___.
的离心率为___. 满足条件
满足条件 则
则 的最大值是
的最大值是 B.
B.  C.
C. D.
D.
