题目内容
已知a、b、c为等比数列,b、m、a和b、n、c是两个等差数列,则
+
=( )
| a |
| m |
| c |
| n |
| A、4 | B、3 | C、2 | D、1 |
分析:由等差数列的性质可得a、b、c与m、n的关系,根据等比数列的定义,用a、q表示b、c,代入所求式子中,整理化简即可.
解答:解:∵b、m、a和b、n、c是两个等差数列,
∴m-b=a-m,n-b=c-n,
∴m=
,n=
;
∵a、b、c为等比数列,设公比为q,
则b=aq,c=aq2,
∴
+
=
+
=
+
=
+
=
=2.
故选C.
∴m-b=a-m,n-b=c-n,
∴m=
| a+b |
| 2 |
| b+c |
| 2 |
∵a、b、c为等比数列,设公比为q,
则b=aq,c=aq2,
∴
| a |
| m |
| c |
| n |
| a | ||
|
| c | ||
|
=
| 2a |
| a+aq |
| 2aq2 |
| aq+aq2 |
=
| 2 |
| 1+q |
| 2q |
| 1+q |
=
| 2+2q |
| 1+q |
故选C.
点评:本题考查了等差数列和等比数列的性质,考查了学生的分析能力与运算能力.

练习册系列答案
相关题目
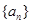 中,
中,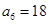 且
且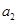 是
是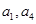 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为