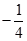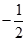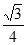题目内容
若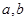 是任意实数,且
是任意实数,且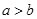 ,则( )
,则( )
A.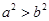 | B. | C.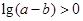 | D.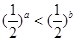 |
D
解析试题分析:因为 是单调减函数,且
是单调减函数,且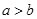 ,所以
,所以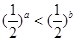 .
.
考点:本小题主要考查函数的单调性.
点评:比较大小时经常用到函数的单调性,必要时要借助0,1等作中间量.

练习册系列答案
相关题目
已知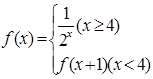 ,则
,则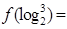 ( )
( )
A.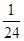 | B.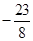 | C.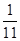 | D.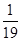 |
函数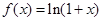 的定义域是( )
的定义域是( )
A.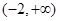 | B.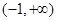 | C.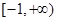 | D.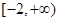 |
若函数 在区间
在区间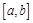 上为减函数,则
上为减函数,则 在
在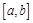 上( ).
上( ).
| A.至少有一个零点 | B.只有一个零点 |
| C.没有零点 | D.至多有一个零点 |
设函数 的定义域为实数集R,
的定义域为实数集R, ,且当
,且当 时,
时, ,则有( )
,则有( )
A.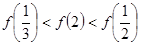 | B. |
C. | D. |
函数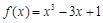 在闭区间 [-3,0] 上的最大值、最小值分别是( )
在闭区间 [-3,0] 上的最大值、最小值分别是( )
| A.1,? 1 | B.1,? 17 | C.3,? 17 | D.9,? 197 |
函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于
| A.8 | B.6 | C.4 | D.2 |
定义在R上的偶函数f(x)的一个单调递增区间为(3,5),则y=f(x-1)
| A.图象的对称轴为x=-1,且在(2,4)内递增 |
| B.图象的对称轴为x=-1,且在(2,4)内递减 |
| C.图象的对称轴为x=1,且在(4,6)内递增 |
| D.图象的对称轴为x=1,且在(4,6)内递减 |
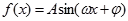 (
(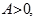
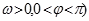 的部分图像如图所示.若△EFG为等腰直角三角形,且
的部分图像如图所示.若△EFG为等腰直角三角形,且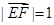 ,则
,则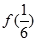 的值为 ( )
的值为 ( )