题目内容
某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
|
版本 |
人教A版 |
人教B版 |
||
|
性别 |
男教师 |
女教师 |
男教师 |
女教师 |
|
人数 |
6 |
|
4 |
|
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是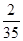 .且
.且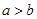 .
.
(1)求实数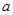 ,
,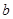 的值
的值
(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为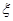 ,求随机变量
,求随机变量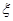 的分布列和数学期望
的分布列和数学期望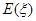 .
.
(1) (2)
(2) 的分布列为
的分布列为
|
|
0 |
1 |
2 |
|
|
|
|
|
故数学期望
【解析】
试题分析:解:(1)从15名教师中随机选出2名共 种选法, 所以这2人恰好是教不同版本的女教师的概率是
种选法, 所以这2人恰好是教不同版本的女教师的概率是 . 计算可得
. 计算可得 ,且
,且 ,则
,则
(2)由题意得
 ;
;  ;
;
故 的分布列为
的分布列为
|
|
0 |
1 |
2 |
|
|
|
|
|
故数学期望
考点:分布列和数学期望
点评:分布列是求出数学期望的前提,因而需写好分布列,而分布列关键是求出概率,当写完分布列,可以结合概率总和为1的特点检验分布列是否正确。

 阅读快车系列答案
阅读快车系列答案(本小题满分12分)
某市举行一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
|
版本 |
人教A版 |
人教B版 |
||
|
性别 |
男教师 |
女教师 |
男教师 |
女教师 |
|
人数 |
6 |
3 |
4 |
2 |
(1)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为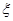 ,求随机变量
,求随机变量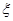 的分布列和数学期望
的分布列和数学期望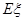 .
.
某市举行一次数学新课程骨干培训,共邀请15名使用不同版本教材的教师,数据如下表所示:
版本 | 人教A版 | 人教B版 | ||
性别 | 男教师 | 女教师 | 男教师 | 女教师 |
人数 | 6 | 3 | 4 | 2 |
(1)从这15名教师中随机选出2名,则2人恰好是教不同版本的男教师的概率是多少?
(2)培训活动随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(本小题满分12分)
某市举行一次数学新课程培训,共邀请15名研究不同版本教材的骨干教师,数据如下表所示:
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 | 3 | 4 | 2 |
(Ⅰ)从这15名教师中随机选出2名,则2人恰好是研究不同版本教材的男教师的概率是多少?
(Ⅱ)培训活动随机选出2名代表发言,设发言代表中研究人教B版教材的女教师人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.




