题目内容
如图所示,在三棱柱ABC-A1B1C1中,侧面A1ABB1和BCC1B1是两个全等的正方形,AC1⊥平面A1DB,D为AC的中点.
(Ⅰ)求证:平面A1ABB⊥平面BCC1B1;
(Ⅱ)求证:B1C∥平面A1DB;
(Ⅲ)设E是CC1上一点,试确定点E的位置,使平面A1DB⊥平面BDE,并说明理由.
(Ⅰ)求证:平面A1ABB⊥平面BCC1B1;
(Ⅱ)求证:B1C∥平面A1DB;
(Ⅲ)设E是CC1上一点,试确定点E的位置,使平面A1DB⊥平面BDE,并说明理由.

(Ⅰ)解法一:∵AC1⊥平面A1DB,A1B 平面A1DB, 平面A1DB,∴AC1⊥A1B, 又在正方形A1ABB1中,A1B⊥AB1,AC1∩AB1=A, ∴A1B⊥面AC1B1, 又B1C1  面AC1B1, 面AC1B1,∴ A1B⊥B1C1, 又在正方形BCC1B1中有,B1C1⊥BB1, 又BB1∩A1B=B, ∴B1C1⊥平面A1ABB1,B1C1  平面B1BCC1, 平面B1BCC1,∴平面A1ABB1⊥平面BCC1B1。 解法二:由已知可知三棱柱是直三棱柱, ∴四边形A1ACC1为矩形, 又AC1⊥平面A1DB,A1D  平面A1DB, 平面A1DB, ∴AC1⊥A1D, 又D为AC的中点, ∴由平面几何知识可知,△A1AD~△ACC1, ∴AA1:AD=AC:CC1,AC2= AA1·CC1=AB2, ∴AC=  AB, AB, ∴AB⊥BC, 又BC⊥BB1且BB1∩AB=B, ∴BC⊥平面A1ABB1,BC  平面BCC1B1, 平面BCC1B1, ∴平面A1ABB1⊥平面BCC1B1。 |
|
|
(Ⅱ)解法一:由(Ⅰ)知BC,BB1,BA两两垂直, |
 |
| (Ⅲ)解法一:设点E(1,b,0),平面BDE的法向量为m=(x,y,z), 则有  , 得 , 得 , ,令y=l,则m=(-b,1,b), 由m·n=(1,1,-1)·(-b,1,b)=0,得b=  , ,即当E为CC1中点时,平面A1BD⊥平面BDE。 解法二:取CC1中点E, D为AC中点, 在△ACC1中, ∴DE∥AC1, 又AC1⊥平面A1DB, ∴DE⊥平面A1DB,DE  平面BDE, 平面BDE,∴平面A1DB⊥平面BDE, 即当E为CC1中点时,平面A1DB⊥平面BDE。 |
 |

练习册系列答案
相关题目
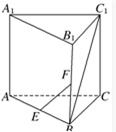 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、60° | C、90° | D、120° |
 ,
, ,
, ,
, ,
, ,
, 平面A1DB,
平面A1DB, 平面A1DB。
平面A1DB。 平面A1DB1,OD
平面A1DB1,OD 平面A1DB,
平面A1DB,  如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心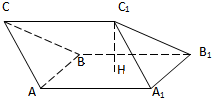 如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心
如图所示,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心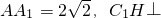 平面AA1B1B且
平面AA1B1B且 .
.
