题目内容
函数f(x)=tan(x+ ),g(x)=
),g(x)=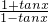 ,h(x)=cot(
,h(x)=cot( -x)其中为相同函数的是
-x)其中为相同函数的是
- A.f(x)与g(x)
- B.g(x)与h(x)
- C.h(x)与f(x)
- D.f(x)与g(x)及h(x)
C
分析:判断两个函数为相同函数的方法是:对应法则相同且定义域相同.利用两角和的正切函数公式及诱导公式可将三个关系式化相同,根据正切函数的定义求出的自变量范围g(x)、f(x)和h(x),所以得到f(x)与h(x)为相同函数.
解答:g(x)=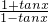 =
= =tan(x+
=tan(x+ )且tanx≠1;h(x)=cot(
)且tanx≠1;h(x)=cot( -x)=cot[
-x)=cot[ -(x+
-(x+ )]=tan(x+
)]=tan(x+ )
)
f(x)的定义域为:x+ ≠kπ+
≠kπ+ 即x≠kπ+
即x≠kπ+ ;g(x)的定义域为x≠kπ+
;g(x)的定义域为x≠kπ+ 且x≠kπ+
且x≠kπ+ ;h(x)的定义域为x≠kπ+
;h(x)的定义域为x≠kπ+ .
.
所以f(x)和h(x)为相同函数.
故选C
点评:考查学生灵活运用两个和的正切函数公式及诱导公式化简求值,掌握相同函数的判别方法.
分析:判断两个函数为相同函数的方法是:对应法则相同且定义域相同.利用两角和的正切函数公式及诱导公式可将三个关系式化相同,根据正切函数的定义求出的自变量范围g(x)、f(x)和h(x),所以得到f(x)与h(x)为相同函数.
解答:g(x)=
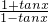 =
= =tan(x+
=tan(x+ )且tanx≠1;h(x)=cot(
)且tanx≠1;h(x)=cot( -x)=cot[
-x)=cot[ -(x+
-(x+ )]=tan(x+
)]=tan(x+ )
)f(x)的定义域为:x+
 ≠kπ+
≠kπ+ 即x≠kπ+
即x≠kπ+ ;g(x)的定义域为x≠kπ+
;g(x)的定义域为x≠kπ+ 且x≠kπ+
且x≠kπ+ ;h(x)的定义域为x≠kπ+
;h(x)的定义域为x≠kπ+ .
.所以f(x)和h(x)为相同函数.
故选C
点评:考查学生灵活运用两个和的正切函数公式及诱导公式化简求值,掌握相同函数的判别方法.

练习册系列答案
相关题目
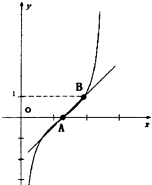 如图为函数f(x)=tan(
如图为函数f(x)=tan(