题目内容
在△ABC中，已知tanA=m，则A等于( )A.arctanm
B.π-arctanm
C.当m＞0时，A=arctanm，当m＜0时，A=π-arctanm
D.当m＞0时，A=arctanm，当m＜0时，A=π+arctanm
思路分析：首先对m分类，根据m值的正负来确定角的终边位置，进而利用反正切来表示角.
由于A是三角形内角，则当m＞0时，A是锐角，则A=arctanm，当m＜0时，A是钝角，此时不能直接用反正切表示.但此时A-π∈(
, 
)，则A-π可用反正切表示，又由正切函数的性质可知tan(A-π)=tanA=m，所以A-π=arctanm，则?A=π+arctanm，故选择D.
答案：D
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
)
是△ABC的垂心，且
．
的直线与轨迹M交于点P，点Q(t，0)是x轴上任意一点，
，H是△ABC的垂心，且
．
的直线与轨迹M交于点P，点Q（t，0）是x轴上任意一点，求当△CPQ为锐角三角形时t的取值范围．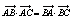
．
｜＝｜
｜；
，求｜
－t