题目内容
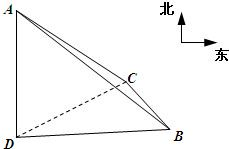为测量某塔的高度，同学甲先在观察点C测得塔顶A在南偏西80°方向上，仰角为45°，然后沿南偏东40°方向前进30米到B点后，测得塔顶A仰角为30°，试根据同学甲测得的数据计算此塔AD的高度．（其中点A为塔顶，点D为塔顶A在地面上的射影，点B、C、D均在地面上，不考虑同学甲的身高）
分析：设出AD=x，进而根据题意可表示出BD，DC，进而在△DBC中利用余弦定理建立方程求得x．
解答：
解：由题可设AD=x，则BD=
x ， DC=x
在△DBC中，∠BCD=120°，BC=30，由余弦定理得BD2=BC2+CD2-2BC•CD•cos∠DCB
即：3x2=302+x2-2×30•x•cos120°
整理得：x2-15x-450=0
解得x=30或x=-15（舍）
所以，所求塔高为30米
解：由题可设AD=x，则BD=| 3 |
在△DBC中，∠BCD=120°，BC=30，由余弦定理得BD2=BC2+CD2-2BC•CD•cos∠DCB
即：3x2=302+x2-2×30•x•cos120°
整理得：x2-15x-450=0
解得x=30或x=-15（舍）
所以，所求塔高为30米
点评：本题主要考查了解三角形的实际应用．考查了运用数学知识，建立数学模型解决实际问题的能力．
练习册系列答案
计算高手系列答案
相关题目
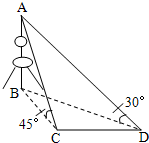如图所示，要测量底部不能到达的某电视塔AB的高度，在塔的同一侧选择C、D两观测点，且在C、D两点测得塔顶的仰角分别为45°、30°，在水平面上测得∠BCD=120°，C、D两地相距500m，则电视塔AB的高度是（ ）A、100
| ||
| B、400m | ||
C、200
| ||
| D、500m |