Question

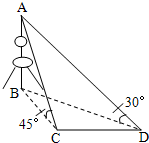如图所示，要测量底部不能到达的某电视塔AB的高度，在塔的同一侧选择C、D两观测点，且在C、D两点测得塔顶的仰角分别为45°、30°，在水平面上测得∠BCD=120°，C、D两地相距500m，则电视塔AB的高度是（　　）

• A、100

  2

  m
• B、400m
• C、200

  3

  m
• D、500m

Answer 1

分析：先求出BC，BD，再在△BCD中，由余弦定理可得结论．

解答：解：设塔高AB=hm，在Rt△ABC中，
由已知BC=hm，在Rt△ABD中，由已知BD=

3

hm，
在△BCD中，
由余弦定理可得3h²=h²+500²-2h•500•cos120°，
即h²-250h-125000=0，
解得h=500（m）（负值舍去）．
故选D．

点评：本题考查余弦定理的运用，考查学生的计算能力，正确运用余弦定理是关键．