题目内容
在数列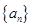 中,
中,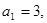
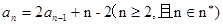
(1)求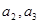 的值;
的值;
(2)证明:数列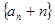 是等比数列,并求
是等比数列,并求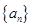 的通项公式;
的通项公式;
(3)求数列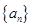 的前n项和
的前n项和 .
.
(1) ;(2)证明详见解析,
;(2)证明详见解析, ;(3)
;(3) .
.
解析试题分析:(1)赋值:令 ;(2)涉及到等差数列,等比数列的证明问题,只需按照定义证明即可,∴利用等比数列的定义证明,利用等比数列通项公式可求出
;(2)涉及到等差数列,等比数列的证明问题,只需按照定义证明即可,∴利用等比数列的定义证明,利用等比数列通项公式可求出
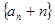 的通项公式,从而求出
的通项公式,从而求出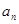 ;(3)根据通项公式求
;(3)根据通项公式求 ,常用方法有裂项相消法,错位相减法,分组求和法,奇偶并项求和法.
,常用方法有裂项相消法,错位相减法,分组求和法,奇偶并项求和法.
试题解析:(1)令 ,
, 令
令 ,
, .
.
(2) ,∴数列
,∴数列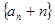 是首项为4,公比为2的等比数列,∴
是首项为4,公比为2的等比数列,∴ .
.
(3)∵数列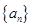 的通项公式
的通项公式 ,∴
,∴
 .
.
考点:1、赋值法;2、等比数列的定义;3、分组求和法求数列前 项和.
项和.

练习册系列答案
相关题目
 (S2n+S2m)-(n-m)2,其中m,n为任意正整数.
(S2n+S2m)-(n-m)2,其中m,n为任意正整数. -
-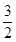 an+33=k2的所有正整数k,n.
an+33=k2的所有正整数k,n.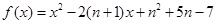 .
. 的图像的顶点的纵坐标构成数列
的图像的顶点的纵坐标构成数列 ,求证:
,求证: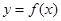 的图像的顶点到
的图像的顶点到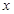 轴的距离构成数列
轴的距离构成数列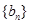 ,求
,求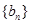 的前
的前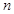 项和
项和 .
. 的首项
的首项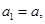 其中
其中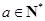 ,
,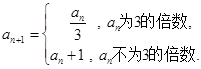 令集合
令集合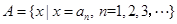 .
.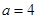 ,写出集合
,写出集合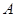 中的所有的元素;
中的所有的元素;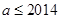 ,且数列
,且数列 的所有可能取值构成的集合;
的所有可能取值构成的集合;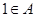 .
.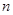 年该生产线设备低劣化值为
年该生产线设备低劣化值为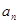 ,求
,求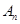 ,当
,当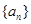 的前
的前 项和为
项和为 ,
,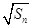 是
是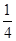 与
与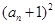 的等比中项.
的等比中项.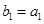 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前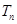 .
.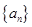 满足:
满足: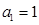 ,
,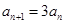 ,
,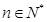 .
. 项和
项和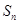 ;
;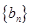 是等差数列,
是等差数列,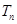 为前
为前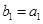 ,
,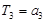 .求
.求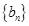 的通项公式,并证明:
的通项公式,并证明: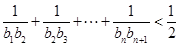 .
.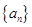 中,
中,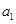 、
、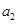 、
、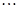 、
、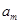 构成首项为2,公差为-2的等差数列,
构成首项为2,公差为-2的等差数列, 、
、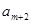 、
、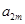 ,构成首项为
,构成首项为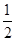 ,公比为
,公比为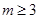 ,
,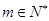 .
.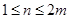 ,
,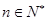 ,都有
,都有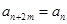 成立.
成立.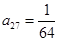 时,求
时,求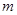 的值;
的值;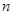 项和为
项和为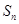 .判断是否存在
.判断是否存在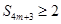 成立?若存在,求出
成立?若存在,求出 的公差为
的公差为 ,且
,且 成等比数列.
成等比数列. ,求数列
,求数列 的前
的前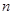 项和
项和 .
.