题目内容
(本题满分15分)
已知偶函数 满足:当
满足:当 时,
时,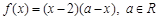 ,当
,当 时,
时,
(1) 求当 时,
时, 的表达式;
的表达式;
(2) 若直线 与函数
与函数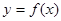 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。
(3) 试讨论当实数 满足什么条件时,函数
满足什么条件时,函数 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
【答案】
(1)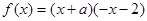
(2)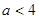
(3)
①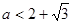 时,
时,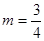
②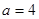 时,
时,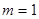
③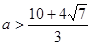 时,
时,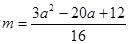 符合题意
符合题意
【解析】、解:(1)设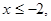 则
则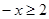 ,
,
又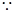 偶函数
偶函数
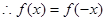
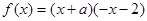 ………………………………………2分
………………………………………2分
(2)(Ⅰ)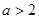 时
时
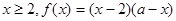
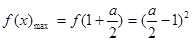
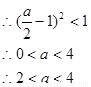
(Ⅱ)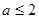 时,都满足
时,都满足
综上,所以
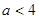 ……………………………………2分
……………………………………2分
(3)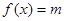 零点
零点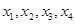 ,
,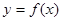 与
与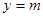 交点4个且均匀分布
交点4个且均匀分布
(Ⅰ)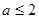 时
时
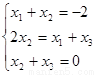 得
得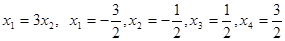 ……2分
……2分
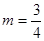
(Ⅱ)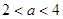 时,
时,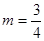 时
时
且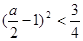
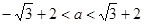 …………………………………2分
…………………………………2分
所以
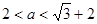 时,
时,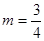
(Ⅲ)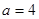 时m=1时
…………………………………1分
时m=1时
…………………………………1分
(IV)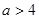 时,
时,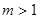
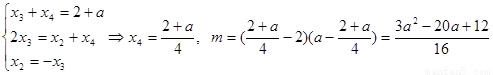
此时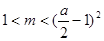
所以
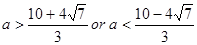 (舍)
(舍)
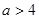 且
且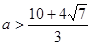 时,
时,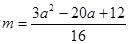 时存在 ………2分
时存在 ………2分
综上:
①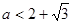 时,
时,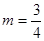
②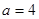 时,
时,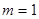
③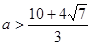 时,
时,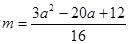 符合题意………1分
符合题意………1分

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 .
. 在
在 上单调递增,在
上单调递增,在 上单调递减,求实数
上单调递减,求实数 的最大值;
的最大值; 对任意的
对任意的 ,
, 都成立,求实数
都成立,求实数 的取值范围.
的取值范围. 为自然对数的底数.
为自然对数的底数. 与曲线
与曲线 相切
相切 在
在 上恰有两个不等的实数根
上恰有两个不等的实数根 ,求
,求 的大小
的大小 :
: (
( ),焦点为
),焦点为 ,直线
,直线 交抛物线
交抛物线 、
、 两点,
两点, 是线段
是线段 的中点,
的中点, 轴的垂线交抛物线
轴的垂线交抛物线 ,
, 到焦点
到焦点 ,求此时
,求此时 的值;
的值; 是以
是以

 的单调区间;
的单调区间; ,若
,若 在
在 上不单调且仅在
上不单调且仅在 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.