题目内容
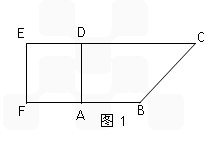
如图(1)在直角梯形PDCB中,PD∥CB,CD⊥PD,PD=6,BC=3,DC=
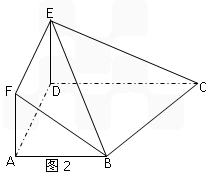
,A是线段PD的中点,E是线段AB的中点;如图(2),沿AB把平面PAB折起,使二面角P-CD-B成45°角.
(1)求证PA⊥平面ABCD;
(2)求平面PEC和平面PAD所成的锐二面角的大小.

| 6 |
(1)求证PA⊥平面ABCD;
(2)求平面PEC和平面PAD所成的锐二面角的大小.

证明:(1)∵AB⊥PA,AB⊥AD
∴AB⊥平面PAD(2分)
∵AB∥DC∴DC⊥平面PAD,
DC⊥PD,DC⊥AD
∴∠PDA是二面角P-CD-B的平面角,故∠PDA=45°(4分)
∵PA=AD=3,∠PDA=45°,∴PA⊥AD
又∵PA⊥AB,∴PA⊥平面ABCD(6分)

(2)如图建立空间直角坐标系A-xyz,
则A(0,0,0),B(
,0,0),C(
,3,0),
D(0,3,0),P(0,0,3),E(
,0,0)(8分)
由(1)知
=(
,0,0)是平面PAD的法向量,
设平面PEC的法向量为
=(x,y,z),
则
,得
(10分)
由
,
令z=1得
=(
,-1,1),(12分)
设向量
与
所成的角为θ,
则:cosθ=
=
=
∴向量
与
所成的角为30°,(13分)
故平面PEC和平面PAD所成的二面角为30°.(14分)
∴AB⊥平面PAD(2分)
∵AB∥DC∴DC⊥平面PAD,
DC⊥PD,DC⊥AD
∴∠PDA是二面角P-CD-B的平面角,故∠PDA=45°(4分)
∵PA=AD=3,∠PDA=45°,∴PA⊥AD
又∵PA⊥AB,∴PA⊥平面ABCD(6分)

(2)如图建立空间直角坐标系A-xyz,
则A(0,0,0),B(
| 6 |
| 6 |
D(0,3,0),P(0,0,3),E(
| ||
| 2 |
由(1)知
| AB |
| 6 |
设平面PEC的法向量为
| n |
则
|
|
由
|
令z=1得
| n |
| 6 |
设向量
| AB |
| n |
则:cosθ=
| ||||
|
|
(
| ||||
|
| ||
| 2 |
∴向量
| AB |
| n |
故平面PEC和平面PAD所成的二面角为30°.(14分)

练习册系列答案
相关题目
 AD且AB=AD=
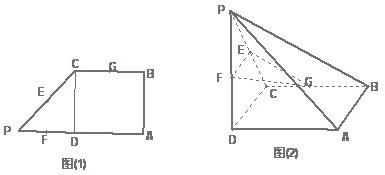
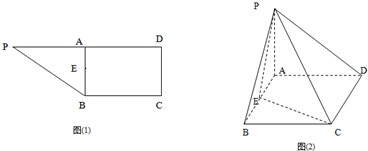
AD且AB=AD=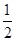 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
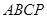 中,
中,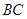 ∥
∥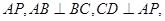
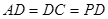 =2,
=2,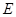 、
、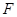 、
、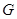 分别是
分别是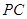 、
、 、
、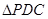 沿
沿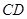 折起,使平面
折起,使平面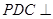 平面
平面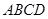 (如图2).
(如图2). 的大小;
的大小;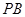 上确定一点
上确定一点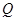 ,使
,使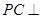 平面
平面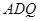 ,并给出证明过程.
,并给出证明过程.
 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。