题目内容
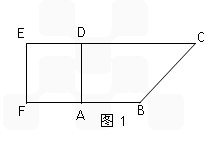
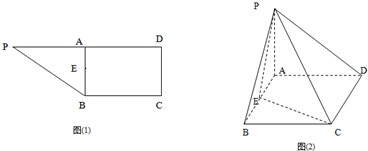
如图(1)在直角梯形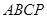 中,
中,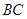 ∥
∥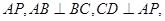
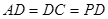 =2,
=2,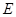 、
、 、
、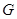 分别是
分别是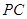 、
、 、
、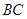 的中点,现将
的中点,现将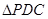 沿
沿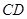 折起,使平面
折起,使平面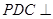 平面
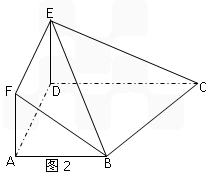
平面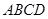 (如图2).
(如图2).
(Ⅰ)求二面角 的大小;
的大小;
(Ⅱ)在线段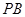 上确定一点
上确定一点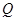 ,使
,使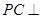 平面
平面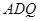 ,并给出证明过程.
,并给出证明过程.
 |
【答案】
 ,点
,点 是线段
是线段 的中点
的中点
【解析】解:
取 的中点
的中点 ,连
,连 、
、 ,
, ∥
∥ ,
,
 又平面
又平面  平面
平面 ,且
,且 ,
,
 平面
平面 ,又
,又 平面
平面 ,由三垂线定理,得
,由三垂线定理,得 ,
,
 就是二面角
就是二面角 的平面角.
的平面角.
在 中,
中,
 ,
,
即二面角 的大小为
的大小为 .
.
(2)当点 是线段
是线段 的中点时,有
的中点时,有
 平面
平面 .证明过程如下:
.证明过程如下:
 为
为 的中点,
的中点, ∥
∥ ,又
,又 ∥
∥ ,
, ∥
∥ ,
,
从而 、
、 、
、 、
、 四点共面.
四点共面.
在 中,
中, 为
为 的中点,
的中点, ,
,
又 平面
平面 ,
, ,
, ,又
,又 ,
,
 平面
平面 ,即
,即 平面
平面 .
.
 解法二:
解法二:
(1)建立如图所示的空间直角坐标系
则

设平面 的法向量为
的法向量为 ,则
,则
 ,取
,取
又平面 的法向量为
的法向量为
所以
 即二面角
即二面角 的大小为
的大小为 .
.
(2)设 则
则

又 ,
, 平面
平面

 点
点 是线段
是线段 的中点.
的中点.

练习册系列答案
相关题目
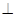 AD且AB=AD=
AD且AB=AD=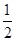 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。