题目内容

知A、B、C是锐角△ABC的三个内角，向量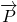 $数学公式$ =（1+sinA，1+cosA）， $数学公式$ =（1+sinB，-1-cosB），则 $数学公式$ 与 $数学公式$ 的夹角是

A.
锐角
B.
钝角
C.
直角
D.
不确定

A
分析：A、B、C是锐角△ABC的三个内角，推出sinA＞cosB＞0，sinB＞cosA＞0，求出数量积值的符号，可以判断 $\text{[math]}$ 与 $\text{[math]}$ 的夹角．
解答：锐角△ABC中，sinA＞cosB＞0，sinB＞cosA＞0，
故有 $\text{[math]}$ • $\text{[math]}$ =（1+sinA）（1+sinB）-（1+cosA）（1+cosB）＞0，
同时易知 $\text{[math]}$ 与 $\text{[math]}$ 方向不相同，故 $\text{[math]}$ 与 $\text{[math]}$ 的夹角是锐角．
故选A．
点评：本题考查数量积表示两个向量的夹角，考查计算能力，是基础题．

练习册系列答案

课时练优选卷系列答案

金榜小状元系列答案

单元自测题同步达标测试卷系列答案

小考练兵场系列答案

创新设计高考总复习系列答案

魔法教程课本诠释与思维拓展训练系列答案

北京市小学毕业考试考试说明系列答案

晨读晚练系列答案

小学毕业考试试卷精编系列答案

新课程学习资源学习手册系列答案

相关题目

已知a，b，c是锐角△ABC中∠A，∠B，∠C的对边，若a=3，b=4，△ABC的面积为3

已知A、B、C是锐角△ABC的三个内角，向量

=(1，cosB)，则

的夹角是（　　）

已知A、B、C是锐角，求证：cosA+cosB+cosC=1+4sin

的充要条件是A+B+C=π．

已知命题p：若a，b∈R，则|a|+|b|＞1是|a+b|＞1的充分不必要条件；命题q：已知A，B，C是锐角三角形ABC的三个内角；向量

=(1+sinA，1+cosA)，

=(1+sinB，-1-cosB)，则

的夹角是锐角．则（　　）

A、p假q真	B、P且q为真
C、p真q假	D、p或q为假

已知A、B、C是锐角△ABC的三个内角，向量

=(1，cosB)，则

的夹角是（　　）