题目内容
已知a,b,c是锐角△ABC中∠A,∠B,∠C的对边,若a=3,b=4,△ABC的面积为3| 3 |
分析:首先利用三角形的面积公式求出sinC,再利用同角三角函数的基本关系式求出cosC,最后根据余弦定理求解即可.
解答:解:∵s=
absinC,a=3,b=4,△ABC的面积为3
,
∴3
=
×3×4×sinC,
解得sinC=
,
∵∠C是锐角,
∴cosC=
=
,
∴c2=a2+b2-2abcosC=13,
∴c=
,
故答案为
.
| 1 |
| 2 |
| 3 |
∴3
| 3 |
| 1 |
| 2 |
解得sinC=
| ||
| 2 |
∵∠C是锐角,
∴cosC=
| 1-sin2C |
| 1 |
| 2 |
∴c2=a2+b2-2abcosC=13,
∴c=
| 13 |
故答案为
| 13 |
点评:本题考查了三角形的面积公式、同角三角函数的基本关系式、余弦定理等基础知识,考查了基本运算能力.

练习册系列答案
相关题目
已知A、B、C是锐角△ABC的三个内角,向量
=(-sinA,1)
=(1,cosB),则
与
的夹角是( )
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |
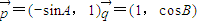 ,则
,则 的夹角是( )
的夹角是( )