Question

【题目】集合由满足以下性质的函数组成：①在上是增函数；②对于任意的， .已知函数， .

（1）试判断， 是否属于集合，并说明理由；

（2）将（1）中你认为属于集合的函数记为.

（ⅰ）试用列举法表示集合；

（ⅱ）若函数在区间上的值域为，求实数 的取值范围．

Answer 1

【答案】(1)见解析；（2）(i) ;(ii) 实数的取值范围是.

【解析】试题分析: （1）通过特例，判断不在集合中，判断的单调性,求出的值域，即可判断是否在集合中；

（2）（ⅰ）利用 （1）在集合中，解指数方程，即可得到集合．

试题解析:（1）因为，不满足②，所以不属于集合．

(ii)由（1）知， 在上单调增，所以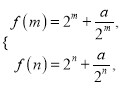

所以方程在内有两个不等的实根，解之即可得到实数的取值范围.

在内任取两个数， ，设，

则，

因为是单调增函数，且，所以， ，

所以，即，

故在上是增函数，满足①；

所以在上的值域为，满足②．

故函数属于集合．

（2）(i)由（1）知， ，所以，

即，解得或，

所以或，故．

(ii)由（1）知， 在上单调增，所以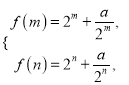

所以方程在内有两个不等的实根，

所以解得．

故实数的取值范围是．