题目内容
函数y=f(x)的图象如图1-6-8所示,则y=f(x)的解析式为( )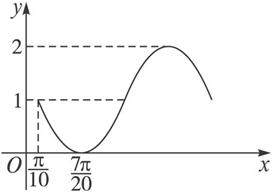
图1-6-8
A.y=sin2x-2 B.y=2cos3x-1
C.y=sin(2x-
)-1 D.y=1-sin(2x-
)
解析:A=
=1,b==1,
.
∴T=π,ω=
=
=2.
∴y=sin(2x+φ)+1,
x=
,2x+φ=-π.
∴φ=-π-
.
∴y=sin(2x-π-
)+1
=-sin(π-2x+
)+1
=sin(-2x+
)+1
=-sin(2x-
)+1.
答案:D
练习册系列答案
相关题目
已知函数y=f(x)的图象和y=sin(x+
)的图象关于点P(
，0)对称，现将f（x）的图象向左平移
个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y=g（x）的图象，则y=g（x）的表达式为（ ）
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
A、y=-sin
| ||
B、y=-cos
| ||
C、y=-sin(4x-
| ||
D、y=-cos(4x-
|
（a＞0且a≠1），
对称；
y=f′(x)的图象可能是( )