Question

已知函数f（x）=-（a＞0且a≠1），

（1）证明：函数y=f(x)的图象关于点对称；

（2）求f（-2）+f（-1）+f（0）+f（1）+f（2）+f（3）的值.

Answer 1

（1）证明略（2）-3

解析:

（1）证明  函数f（x）的定义域为R，任取一点（x，y），它关于点对称的点的坐标为（1-x，-1-y）.       2分

由已知得y=-,

则-1-y=-1+=-，                                                                                                                                                 3分

f（1-x）=-=-

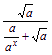
=-=-，                                                                                                             5分

∴-1-y=f（1-x）.

即函数y=f(x)的图象关于点对称.                                                                                        7分

（2）解  由（1）有-1-f（x）=f（1-x），

即f（x）+f（1-x）=-1.

∴f（-2）+f（3）=-1，f（-1）+f（2）=-1，

f（0）+f（1）=-1，

则f（-2）+f（-1）+f（0）+f（1）+f（2）+f（3）=-3.                                                     14分