题目内容
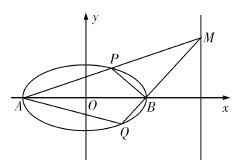
【题目】已知圆![]() :
:![]() ,圆
,圆![]() 与圆
与圆![]() 关于直线
关于直线![]() :
:![]() 对称.
对称.
(1)求圆![]() 的方程;
的方程;
(2)过直线![]() 上的点
上的点![]() 分别作斜率为
分别作斜率为![]() ,4的两条直线
,4的两条直线![]() ,
,![]() ,使得
,使得![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长相等.
截得的弦长相等.
(i)求点![]() 的坐标;
的坐标;
(ii)过点![]() 任作两条互相垂直的直线分别与两圆相交,判断所得弦长是否恒相等,并说明理由.
任作两条互相垂直的直线分别与两圆相交,判断所得弦长是否恒相等,并说明理由.
【答案】(1) ![]() (2) (i)
(2) (i)![]() .(ii)恒相等.见解析
.(ii)恒相等.见解析
【解析】
(1)根据轴对称求得圆![]() 的圆心即可.
的圆心即可.
(2)由题,两问均可设![]() 与过点
与过点![]() 任作两条互相垂直的直线分别为
任作两条互相垂直的直线分别为![]() ,再由题意得
,再由题意得![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离相等,列式求解与证明即可.
的距离相等,列式求解与证明即可.
(1)设![]() ,因为圆
,因为圆![]() 与圆
与圆![]() 关于直线
关于直线![]() :
:![]() 对称,
对称,![]() ,
,
则直线![]() 与直线
与直线![]() 垂直,
垂直,![]() 中点在直线
中点在直线![]() 上,得
上,得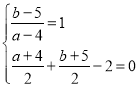 ,
,
解得![]() ,所以圆
,所以圆![]() :
:![]() .
.
(2)(i)设![]() ,
,![]() 的方程为
的方程为![]() ,即
,即![]() ;
;
![]() 的方程为
的方程为![]() ,即
,即![]() .
.
因为![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长相等,且两圆半径相等,
截得的弦长相等,且两圆半径相等,
所以![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离相等,即
的距离相等,即![]() ,
,
所以![]() 或
或![]() .
.
由题意,![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() 不满足题意,舍去,
不满足题意,舍去,
故![]() ,点
,点![]() 坐标为
坐标为![]() .
.
(ii)过点![]() 任作互相垂直的两条直线分别与两圆相交,所得弦长恒相等.
任作互相垂直的两条直线分别与两圆相交,所得弦长恒相等.
证明如下:
当![]() 的斜率等于0时,
的斜率等于0时,![]() 的斜率不存在,
的斜率不存在,![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长都等于圆的直径;
截得的弦长都等于圆的直径;
当![]() 的斜率不存在,
的斜率不存在,![]() 的斜率等于0时,
的斜率等于0时,![]() 与圆
与圆![]() 不相交,
不相交,![]() 与圆
与圆![]() 不相交.
不相交.
当![]() 、
、![]() 的斜率存在且都不等于0,两条直线分别与两圆相交时,设
的斜率存在且都不等于0,两条直线分别与两圆相交时,设![]() 、
、![]() 的方程分别为
的方程分别为
![]() ,
,![]() ,即
,即![]() ,
,![]() .
.
因为![]() 到
到![]() 的距离
的距离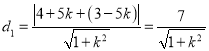 ,
,
![]() 到
到![]() 的距离
的距离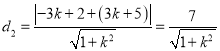 ,所以
,所以![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离相等.
的距离相等.
因为圆![]() 与圆
与圆![]() 的半径相等,所以
的半径相等,所以![]() 被圆
被圆![]() 截得的弦长与
截得的弦长与![]() 被圆
被圆![]() 截得的弦长恒相等.
截得的弦长恒相等.
综上所述,过点![]() 任作互相垂直的两条直线分别与两圆相交,所得弦长恒相等.
任作互相垂直的两条直线分别与两圆相交,所得弦长恒相等.

【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了200名用户,得到用户的满意度评分,现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 |
|
|
|
|
|
频数 | 12 | 28 | 68 |
| 40 |
频率 | 0.06 |
| 0.34 |
| 0.2 |
(1)求表格中的![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计用户的满意度评分的平均数;
(3)若从这200名用户中随机抽取50人,估计满意度评分高于6分的人数为多少?