题目内容
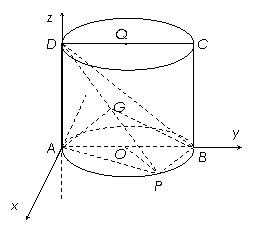
如图,四边形![]() 是圆柱
是圆柱![]() 的轴截面,点
的轴截面,点![]() 在圆柱
在圆柱![]() 的底面圆周上,
的底面圆周上,![]() 是
是![]() 的中点,圆柱
的中点,圆柱![]() 的底面圆的半径
的底面圆的半径![]() ,侧面积为
,侧面积为![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.

(本题考查空间的线面关系、二面角、空间向量及坐标运算、圆柱的侧面积、余弦定理等知识,考查数形结合、化归转化的数学思想和方法,以及空间想象能力、推理论证能力和运算求解能力)
![]() 解: (1)(解法一):由题意可知
解: (1)(解法一):由题意可知 ![]() ,
,
解得 ![]() , …………
, …………![]() 分
分
在![]() 中,
中,
![]() , …………
, …………![]() 分
分
∴ ![]() ,
,
又 ∵![]() 是
是![]() 的中点,
的中点,
∴ ![]() . ① …………
. ① …………![]() 分
分
∵![]() 为圆
为圆![]() 的直径,
的直径,
∴ ![]() .
.
由已知知 ![]() ,
,
∴ ![]() ,
,
∴ ![]() . …………
. …………![]() 分
分
∴ ![]() . ②
. ②
∴ 由①②可知:![]() ,
,
∴ ![]() . …………
. …………![]() 分
分
(2) 由(1)知:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角 . …………
的平面角 . …………![]() 分
分
![]() ,
,
![]() ,
, ![]() .
.
∴ ![]() .
.
![]() . ………
. ………![]() 分
分
(解法二):建立如图所示的直角坐标系,
由题意可知![]() .
.
解得![]() .
.
 则
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴ 可求得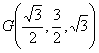 . …………
. …………![]() 分
分
(1)![]() ,
,![]() ,
,
∴ 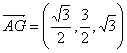 .
.
![]() ∵
∵ 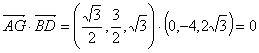 ,
,
∴ ![]() . …………
. …………![]() 分
分
(2)由(1)知,
![]() ,
,
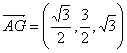 ,
,
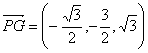 ,
,
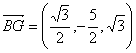 .
.
∵![]() ,
,![]() .
.
∴![]() 是平面
是平面![]() 的法向量. …………
的法向量. …………![]() 分
分
设![]() 是平面
是平面![]() 的法向量,
的法向量,
由![]() ,
,![]() ,
,
解得![]() …………
…………![]() 分
分
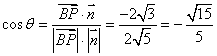 .
.
所以二面角![]() 的平面角的余弦值
的平面角的余弦值![]() . …………
. …………![]() 分
分

 如图所示,圆柱的高为2,底面半径为
如图所示,圆柱的高为2,底面半径为 (2012•韶关一模)如图所示,圆柱的高为2,底面半径为
(2012•韶关一模)如图所示,圆柱的高为2,底面半径为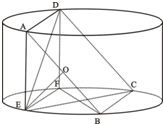 如图所示,圆柱的高为2,底面半径为
如图所示,圆柱的高为2,底面半径为 是圆柱
是圆柱 的轴截面,点
的轴截面,点 在圆柱
在圆柱 是
是 的中点,圆柱
的中点,圆柱 ,侧面积为
,侧面积为 ,
, .
. ;
; 的平面角的余弦值.
的平面角的余弦值.