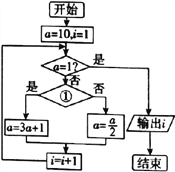
题目内容
【题目】圆x2+y2=1上任意一点P,过点P作两直线分别交圆于A,B两点,且∠APB=60°,则|PA|2+|PB|2的取值范围为___.
【答案】(5,6]
【解析】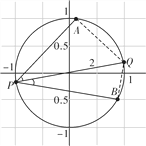
过点P做直径PQ,如图,根据题意可得:|PQ|=2.
令∠APQ=θ,则∠BPQ=![]() -θ.由题意可知:0<θ<
-θ.由题意可知:0<θ<![]() .
.
那么,|PA|=|PQ|cos θ=2cos θ,
|PB|=|PQ|cos![]() =2cos
=2cos![]() .
.
|PA|2+|PB|2=(2cos θ)2+![]() =4
=4![]()
=4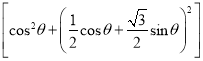 =4cos2θ+
=4cos2θ+![]()
=2cos2θ+2![]() sin θcos θ+3
sin θcos θ+3
=![]() sin 2θ+cos 2θ+4=2
sin 2θ+cos 2θ+4=2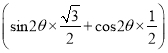 +4
+4
=2sin![]() +4.
+4.
∵0<θ<![]() ,
,
∴0<2θ<![]() ,
,
∴![]() <2θ+
<2θ+![]() <
<![]() ,
,
∴![]() <sin
<sin![]() ≤1.
≤1.
∴5<2sin![]() +4≤6.
+4≤6.
因此,|PA|2+|PB|2的取值范围为(5,6].

练习册系列答案
相关题目