题目内容
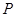 为椭圆
为椭圆 上任意一点,
上任意一点,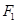 、
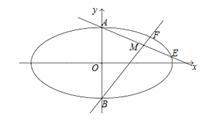
、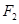 为左右焦点.如图所示:
为左右焦点.如图所示: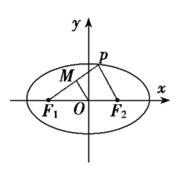
(1)若 的中点为
的中点为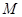 ,求证
,求证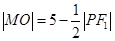 ;
;
(2)若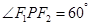 ,求
,求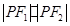 的值.
的值.
(1))证明:在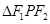 中,
中,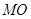 为中位线
为中位线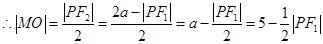
(2)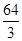
解析试题分析:(1)由椭圆定义知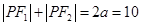 ,则
,则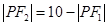 ,由条件知点
,由条件知点 、
、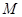 分别是
分别是 、
、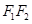 的中点,所以
的中点,所以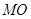 为
为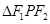 的中位线,则
的中位线,则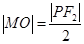 ,从而命题得证;(2)根据椭圆定义,在
,从而命题得证;(2)根据椭圆定义,在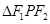 中有
中有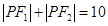 ,
, ,又由条件
,又由条件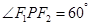 ,从这些信息中可得到提示,应从余弦定理入手,考虑到
,从这些信息中可得到提示,应从余弦定理入手,考虑到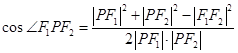 ,所以需将
,所以需将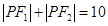 两边平方,得
两边平方,得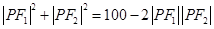 ,将其代入余弦定理,得到关于
,将其代入余弦定理,得到关于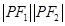 的方程,从而可得解.
的方程,从而可得解.
试题解析:(1)证明:在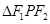 中,
中,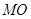 为中位线
为中位线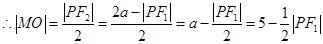 5分
5分
(2)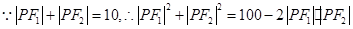 ,
,
在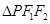 中,
中,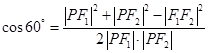 ,
,
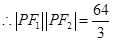 12分
12分
考点:1.椭圆定义;2.余弦定理.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
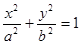 (
(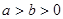 )的右焦点为
)的右焦点为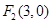 ,离心率为
,离心率为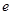 .
.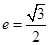 ,求椭圆的方程;
,求椭圆的方程;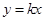 与椭圆相交于
与椭圆相交于 ,
,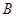 两点,
两点,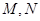 分别为线段
分别为线段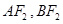 的中点. 若坐标原点
的中点. 若坐标原点 在以
在以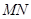 为直径的圆上,且
为直径的圆上,且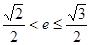 ,求
,求 的取值范围.
的取值范围.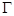 :
: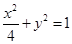 .
.
 (如图),直线
(如图),直线 分别与椭圆
分别与椭圆 两点,其中点
两点,其中点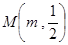 满足
满足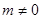 ,且
,且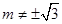 .
.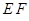 与
与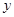 轴交点的位置与
轴交点的位置与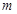 无关;
无关; 面积是∆
面积是∆ 面积的5倍,求
面积的5倍,求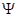 :
: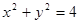 .
.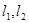 是过点
是过点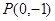 的两条互相垂直的直线,其中
的两条互相垂直的直线,其中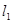 交圆
交圆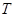 、
、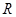 两点,
两点,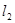 交椭圆
交椭圆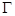 于另一点
于另一点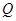 .求
.求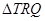 面积取最大值时直线
面积取最大值时直线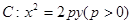 的焦点为
的焦点为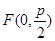 ,准线为
,准线为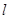 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且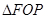 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为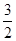 .
.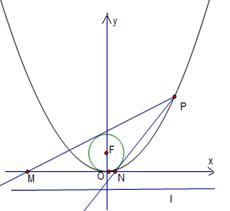
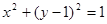 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交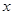 轴于点
轴于点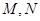 ,求
,求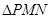 面积的最小值时
面积的最小值时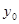 的值.
的值.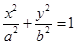
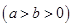 的左、右焦点分别是
的左、右焦点分别是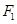 、
、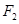 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段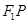 的垂直平分线过点
的垂直平分线过点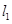 :
: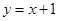 按向量
按向量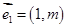 平移后的直线是
平移后的直线是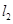 ,直线
,直线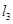 :
: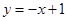 按向量
按向量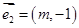 平移后的直线是
平移后的直线是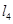 (其中
(其中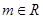 )。
)。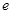 的取值范围。
的取值范围。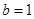 时,求椭圆的方程。
时,求椭圆的方程。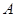 、
、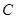 两点,
两点,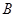 、
、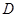 两点。求四边形ABCD面积
两点。求四边形ABCD面积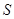 的取值范围。
的取值范围。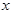 轴对称,它的顶点在坐标原点,点P(1,2),
轴对称,它的顶点在坐标原点,点P(1,2),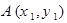 ,
,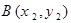 均在抛物线上.
均在抛物线上.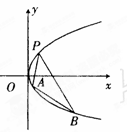
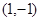 ,求直线AB方程.
,求直线AB方程.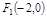 、
、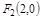 ,动点N满足
,动点N满足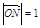 (O为坐标原点),
(O为坐标原点),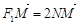 ,
,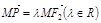 ,
, ,求点P的轨迹方程.
,求点P的轨迹方程.
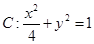 的上、下顶点分别为
的上、下顶点分别为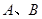 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点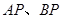 与直线
与直线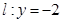 分别交于点
分别交于点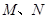 ,
,
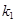 、
、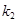 ,求证:
,求证: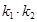 为定值;
为定值; 为直径的圆是否经过定点?请证明你的结论.
为直径的圆是否经过定点?请证明你的结论. ,焦点在
,焦点在 轴上的抛物线过点
轴上的抛物线过点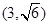 .
.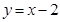 交于
交于 、
、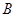 两点,求证:
两点,求证: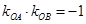 .
.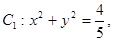 直线
直线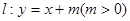 与圆
与圆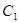 相切,且交椭圆
相切,且交椭圆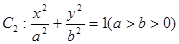 于
于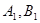 两点,
两点,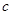 是椭圆的半焦距,
是椭圆的半焦距,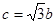 ,
,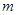 的值;
的值;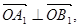 求椭圆
求椭圆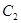 的方程;
的方程;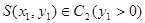 ,直线AS,BS与直线
,直线AS,BS与直线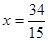 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.