题目内容
(本小题满分12分)
如图,在直三棱柱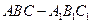 中,
中,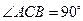 ,
,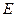 是棱
是棱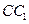 上的动点,
上的动点,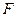 是
是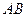 中点,
中点,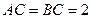 ,
,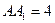 .
.
(Ⅰ)求证: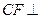 平面
平面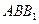 ;
;
(Ⅱ)若二面角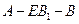 的大小是
的大小是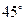 ,求
,求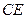 的长.
的长.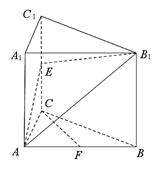
如图,在直三棱柱
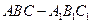 中,
中,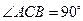 ,
,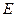 是棱
是棱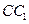 上的动点,
上的动点,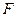 是
是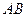 中点,
中点,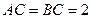 ,
,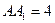 .
.(Ⅰ)求证:
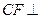 平面
平面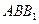 ;
;(Ⅱ)若二面角
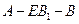 的大小是
的大小是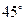 ,求
,求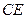 的长.
的长.
(Ⅰ)证明见解析
(Ⅱ)
(Ⅱ)

(Ⅰ)证明:∵三棱柱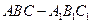 是直棱柱,
是直棱柱,
∴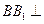 平面
平面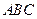 .
.
又∵ 平面
平面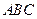 ,∴
,∴
 .
.
∵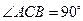 ,
, ,
,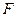 是
是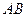 中点,
中点,
∴
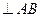 .
.
又∵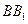 ∩
∩ ,∴
,∴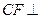 平面
平面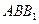 .
.
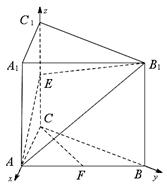
(Ⅱ)解:以 为坐标原点,射线
为坐标原点,射线 为
为 轴正半轴,
轴正半轴,
建立如图所示的空间直角坐标系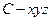 ,
,
则 ,
,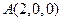 ,
, .
.
设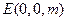 ,平面
,平面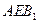 的法向量
的法向量 ,
,
则 ,
,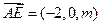 .
.
且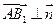 ,
, .
.
于是
所以 取
取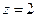 ,则
,则
∵三棱柱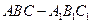 是直棱柱,
是直棱柱,
∴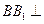 平面
平面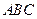 .又∵
.又∵ 平面
平面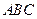 ,
,
∴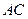
 .∵
.∵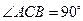 ,
,
∴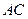
 .∵
.∵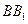 ∩
∩ ,
,
∴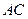
 平面
平面 .
.
∴ 是平面
是平面 的法向量,
的法向量, .
.
∵二面角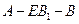 的大小是
的大小是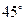 ,
,
∴ .
.
解得 .∴
.∴ .
.
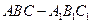 是直棱柱,
是直棱柱,∴
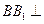 平面
平面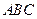 .
.又∵
 平面
平面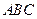 ,∴
,∴
 .
.∵
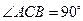 ,
, ,
,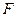 是
是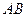 中点,
中点,∴

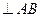 .
.又∵
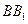 ∩
∩ ,∴
,∴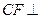 平面
平面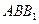 .
.(Ⅱ)解:以
 为坐标原点,射线
为坐标原点,射线 为
为 轴正半轴,
轴正半轴,建立如图所示的空间直角坐标系
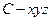 ,
,
则
 ,
,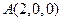 ,
, .
.设
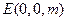 ,平面
,平面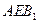 的法向量
的法向量 ,
,则
 ,
,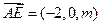 .
.且
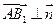 ,
, .
.于是

所以
 取
取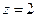 ,则
,则
∵三棱柱
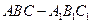 是直棱柱,
是直棱柱,∴
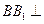 平面
平面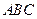 .又∵
.又∵ 平面
平面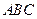 ,
,∴
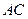
 .∵
.∵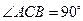 ,
,∴
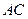
 .∵
.∵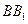 ∩
∩ ,
,∴
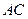
 平面
平面 .
.∴
 是平面
是平面 的法向量,
的法向量, .
.∵二面角
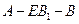 的大小是
的大小是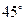 ,
,∴
 .
.解得
 .∴
.∴ .
.
练习册系列答案
相关题目
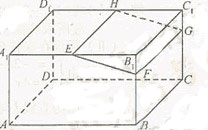
 如图,四棱锥
如图,四棱锥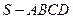 的底面是矩形,
的底面是矩形,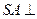 底面
底面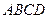 ,P为BC边的中点,SB与
,P为BC边的中点,SB与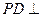 平面SAP;
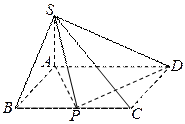
平面SAP;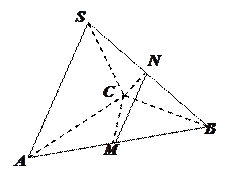 在三棱锥
在三棱锥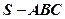 中,
中,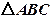 是边长为
是边长为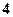 的正三角形,平面
的正三角形,平面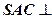 平面
平面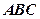 ,
,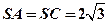 ,
,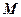 、
、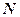 分别为
分别为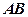 、
、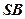 的中点,
的中点,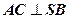 ;
;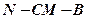 的大小;
的大小;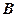 到平面
到平面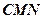 的距离.
的距离.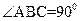 ,
,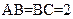 ,二面角P-AB-C为
,二面角P-AB-C为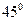 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.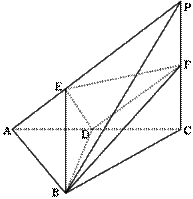
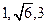 ,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。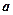 、
、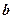 及平面
及平面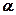 ,给出四个下列命题:
,给出四个下列命题: ,
,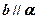 ,则
,则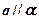 ;
;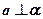 ,
,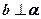 ,则
,则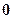 个
个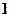 个
个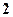 个
个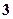 个
个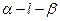 的大小为
的大小为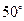 ,
,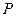 为空间中任意一点,则过点
为空间中任意一点,则过点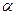 和平面
和平面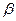 所成的角都是
所成的角都是 的直线的条数为( )
的直线的条数为( )
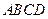 --
--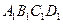 ,E、F分别是
,E、F分别是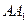 、
、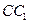 的中点,p是
的中点,p是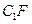 B、线段
B、线段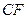 C、线段
C、线段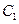 D、线段
D、线段