题目内容
在平面直角坐标系中,O为坐标原点,A(3,0),B(0,1),C是以O为圆心的单位圆上一点,且∠COA= π.
π.(Ⅰ)求
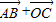 的坐标;
的坐标;(Ⅱ)若直线OC与直线AB交于点D,且
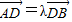 ,求实数λ的值.
,求实数λ的值.
【答案】分析:(I)根据三角函数的定义和单位圆,算出C(-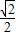 ,
,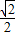 ),由A、B的坐标得到
),由A、B的坐标得到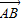 =(-3,1),由此即可得到向量
=(-3,1),由此即可得到向量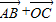 的坐标;
的坐标;
(II)由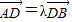 算出D的坐标为(
算出D的坐标为(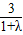 ,
,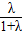 ),代入直线OC方程y=-x得到关于λ的方程,解之即可得到λ的值.
),代入直线OC方程y=-x得到关于λ的方程,解之即可得到λ的值.
解答:解:(I)∵C是以O为圆心的单位圆上一点,
∴设C(cosθ,sinθ),由∠COA= π得cosθ=-
π得cosθ=-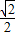 ,sinθ=
,sinθ=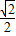
由此可得C(-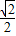 ,
,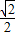 ),
),
∵A(3,0),B(0,1),
∴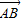 =
=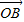 -
-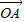 =(-3,1),
=(-3,1),
可得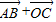 =(-3,1)+(-
=(-3,1)+(-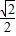 ,
,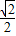 )=(-3-
)=(-3-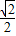 ,1+
,1+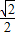 );
);
(II)由(I)得直线OC的方程为y=-x
∵A(3,0),B(0,1),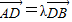 ,
,
∴D的坐标为(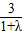 ,
,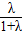 ),
),
代入OC方程得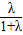 =-
=-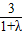 ,得λ=-3
,得λ=-3
点评:本题给出点A、B、C的坐标,求向量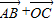 的坐标,并求满足定比分点的λ值.着重考查了向量的坐标运算、三角函数的定义和向量线性运算等知识,属于中档题.
的坐标,并求满足定比分点的λ值.着重考查了向量的坐标运算、三角函数的定义和向量线性运算等知识,属于中档题.
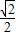 ,
,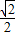 ),由A、B的坐标得到
),由A、B的坐标得到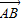 =(-3,1),由此即可得到向量
=(-3,1),由此即可得到向量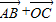 的坐标;
的坐标;(II)由
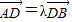 算出D的坐标为(
算出D的坐标为(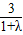 ,
,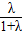 ),代入直线OC方程y=-x得到关于λ的方程,解之即可得到λ的值.
),代入直线OC方程y=-x得到关于λ的方程,解之即可得到λ的值.解答:解:(I)∵C是以O为圆心的单位圆上一点,
∴设C(cosθ,sinθ),由∠COA=
 π得cosθ=-
π得cosθ=-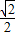 ,sinθ=
,sinθ=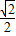
由此可得C(-
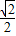 ,
,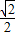 ),
),∵A(3,0),B(0,1),
∴
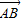 =
=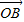 -
-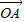 =(-3,1),
=(-3,1),可得
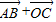 =(-3,1)+(-
=(-3,1)+(-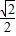 ,
,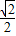 )=(-3-
)=(-3-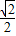 ,1+
,1+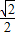 );
);(II)由(I)得直线OC的方程为y=-x
∵A(3,0),B(0,1),
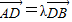 ,
,∴D的坐标为(
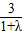 ,
,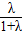 ),
),代入OC方程得
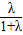 =-
=-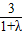 ,得λ=-3
,得λ=-3点评:本题给出点A、B、C的坐标,求向量
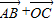 的坐标,并求满足定比分点的λ值.着重考查了向量的坐标运算、三角函数的定义和向量线性运算等知识,属于中档题.
的坐标,并求满足定比分点的λ值.着重考查了向量的坐标运算、三角函数的定义和向量线性运算等知识,属于中档题. 
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目