题目内容
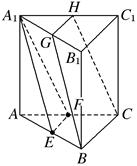
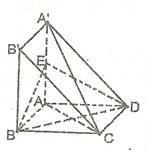
如图,四边形 是正方形,
是正方形,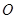 为对角线
为对角线 和
和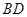 的交点,
的交点,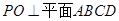 ,
,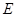 为
为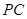 的中点;
的中点;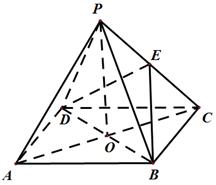
(1)求证: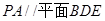 ;
;
(2)求证: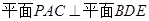 .
.
(1)连接 ,
,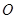 为
为 的中点,所以
的中点,所以 ∵
∵ ∴
∴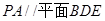 (2)∵
(2)∵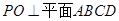 ∴
∴ ∴
∴ ∴
∴ 又∵
又∵ ∴
∴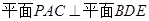
解析试题分析:(1)连接
∵四边形 是正方形,
是正方形,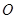 为对角线
为对角线 和
和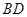 的交点
的交点
∴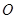 为
为 的中点. 1分
的中点. 1分
又∵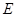 为
为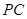 的中点.
的中点.
∴ 为
为 的中位线,即
的中位线,即 . 3分
. 3分
又∵ 4分
4分
∴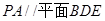 . 5分
. 5分
(2)∵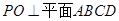
 . 6分
. 6分
∴ . 7分
. 7分
又∵四边形 是正方形
是正方形
∴ . 8分
. 8分
又∵ . 9分
. 9分
∴ . 10分
. 10分
又∵ . 11分
. 11分
∴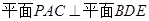 . 12分
. 12分
考点:线面平行的判定与面面垂直的判定
点评:证明线面平行需证平面外一条直线与平面内一条直线平行;证明面面垂直,需证一个平面内的一条直线垂直于另一个平面,即转化为线面垂直

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 与
与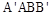 都是边长为
都是边长为 的正方形,点E是
的正方形,点E是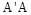 的中点,
的中点,
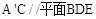 ;
;  ;
;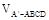 与
与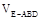 的比值。
的比值。 中,M、N分别是BC、AC1中点,AA1=2,AB=
中,M、N分别是BC、AC1中点,AA1=2,AB=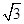 ,AC=AM=1.
,AC=AM=1.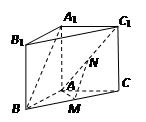
 中,
中,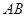 ,
,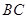 ,
,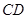 两两互相垂直,且
两两互相垂直,且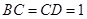 .
.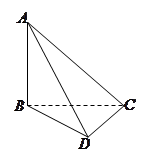
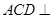 平面
平面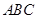 ;
;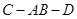 的大小;
的大小; 与平面
与平面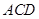 所成的角为
所成的角为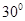 ,求线段
,求线段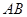 是半圆
是半圆 的直径,
的直径,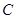 是半圆
是半圆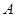 、
、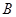 外的一个动点,
外的一个动点, 垂直于半圆
垂直于半圆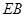 ,
,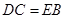 ,
,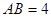 ,
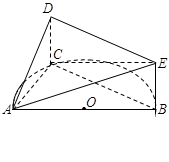
, .
.
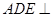 平面
平面 ;
;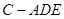 体积最大时,求二面角
体积最大时,求二面角 的余弦值.
的余弦值. 的边长为
的边长为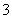 ,点
,点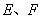 分别在
分别在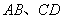 上,并且满足
上,并且满足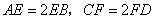 ,如图乙,将直角梯形
,如图乙,将直角梯形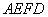 沿
沿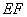 折到
折到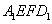 的位置,使点
的位置,使点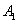 在
在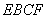 上的射影
上的射影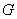 恰好在
恰好在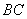 上.
上.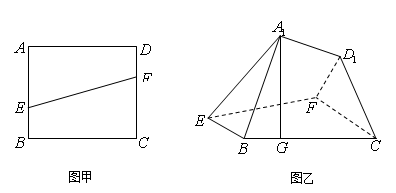
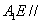 平面
平面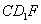 ;
;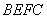 与平面
与平面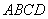 为平行四边形,
为平行四边形,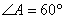 ,
,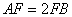 ,
,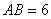 ,点
,点 在
在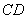 上,
上,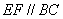 ,
,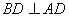 ,
,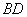 与
与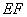 相交于
相交于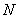 .现将四边形
.现将四边形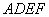 沿
沿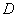 在平面
在平面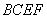 上的射影恰在直线
上的射影恰在直线 上.
上.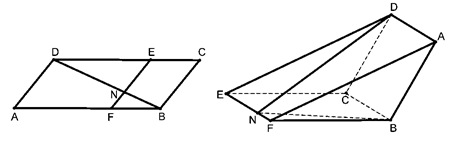
 平面
平面 与平面
与平面 的正方体
的正方体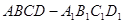 中,
中,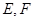 分别为
分别为 的中点.
的中点.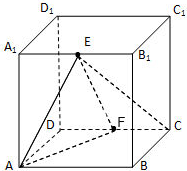
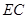 与平面
与平面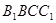 所 成 角的大小;
所 成 角的大小;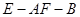 的大小.
的大小.