题目内容
( 13分)已知椭圆![]() ,且C1,C2的公共弦AB过椭圆C1的右焦点。
,且C1,C2的公共弦AB过椭圆C1的右焦点。
(1)求椭圆的焦点坐标及m=0,![]() 时
时![]() 的焦点坐标;
的焦点坐标;
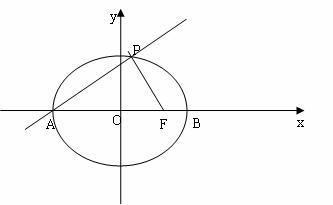
(2)当AB⊥x轴时,判断抛物线C2的焦点是否在直线AB上;
(3)是否存在m,p的值,使抛物线C2的焦点恰在直线AB上?若存在,求出符合条件的m,p的值;若不存在,请说明理由。
( 13分)解:(1)椭圆的焦点坐标(-1,0),(1,0) …………2分
当m=0、![]() 时,
时,
C2的焦点坐标为![]() , …………4分
, …………4分
(2)当AB⊥x轴时,点A、B关于x轴对称,所以m=0。
∵C1的右焦点坐标为(1,0),∴直线AB的方程为x=1。
∴点A的坐标为![]() ,
,
∵点A在抛物线上,![]()
此时,C2的焦点坐标为![]() ,该焦点不在直线AB上。…………8分
,该焦点不在直线AB上。…………8分
(II)假设存在m,p使抛物线C1的焦点恰在直线AB上。
由(I)知直线AB的方程为![]() ,
,
由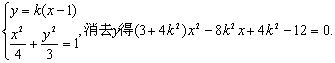 ①
①
设A、B的坐标分别为![]() 是方程①的两个根,
是方程①的两个根,![]()
由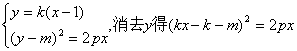 ②
②
![]() ,
,
将③代入②,得![]() ,③
,③
![]() 也是方程③的两个根,
也是方程③的两个根,
![]()
![]() ④
④
又直线AB过C1,C2的焦点,

![]() ⑤
⑤
由④⑤,得![]()
解得![]()
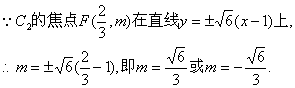
由上可知,满足条件的m,p存在,且![]() …………13分
…………13分 www..com
www..com

练习册系列答案
相关题目
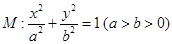 的左右焦点分别为
的左右焦点分别为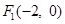 ,
,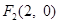 .在椭圆
.在椭圆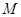 中有一内接三角形
中有一内接三角形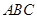 ,其顶点
,其顶点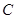 的坐标
的坐标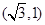 ,
,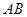 所在直线的斜率为
所在直线的斜率为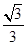 .
. 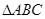 的面积最大时,求直线
的面积最大时,求直线