题目内容
7. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-$\sqrt{6}$,0),e=$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F1(-$\sqrt{6}$,0),e=$\frac{\sqrt{2}}{2}$.(Ⅰ)求椭圆C的方程;
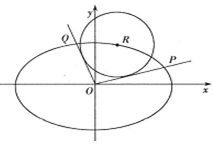
(Ⅱ)如图,设R(x0,y0)是椭圆C上一动点,由原点O向圆(x-x0)2+(y-y0)2=4引两条切线,分别交椭圆于点P,Q,若直线OP,OQ的斜率存在,并记为k1,k2,求证:k1•k2为定值;
(Ⅲ)在(Ⅱ)的条件下,试问OP2+OQ2是否为定值?若是,求出该值;若不是,说明理由.
分析 (Ⅰ)由题意得,c,a,推出b,即可得到椭圆的方程.
(Ⅱ)由已知,直线OP:y=k1x,OQ:y=k2x,且与圆R相切,列出方程,说明k1,k2是方程$k_{\;}^2-2{x_0}{y_0}{k_{\;}}+y_0^2-4=0$的两个不相等的实数根,推出${k_1}{k_2}=\frac{y_0^2-4}{x_0^2-4}$,通过点R(x0,y0)在椭圆C上,化简求解即可.
(Ⅲ)OP2+OQ2是定值18.设直线OP:y=k1x,OQ:y=k2x,联立$\left\{\begin{array}{l}y={k_1}x\\ \frac{x^2}{12}+\frac{y^2}{6}=1\end{array}\right.$解得$x_1^2+y_1^2=\frac{{12({1+k_1^2})}}{1+2k_1^2}$
同理,得$x_2^2+y_2^2=\frac{{12({1+k_2^2})}}{1+2k_2^2}$,然后计算OP2+OQ2=${{x}_{1}}^{2}+{{y}_{1}}^{2}$+${{x}_{2}}^{2}+{{y}_{2}}^{2}$化简求解即可.
解答 (本小题满分12分)
解:(Ⅰ)由题意得,$c=\sqrt{6},e=\frac{{\sqrt{2}}}{2}$,解得$a=2\sqrt{3}$,b=$\sqrt{{a}^{2}-{c}^{2}}$=$\sqrt{6}$…(1分)
∴椭圆方程为$\frac{x^2}{12}+\frac{y^2}{6}=1$…(3分)
(Ⅱ)由已知,直线OP:y=k1x,OQ:y=k2x,且与圆R相切,
∴$\frac{{|{{k_1}{x_0}-{y_0}}|}}{{\sqrt{1+k_1^2}}}=2$,化简得$({x_0^2-4})k_1^2-2{x_0}{y_0}{k_1}+y_0^2-4=0$
同理$({x_0^2-4})k_2^2-2{x_0}{y_0}{k_2}+y_0^2-4=0$,…(5分)
∴k1,k2是方程$k_{\;}^2-2{x_0}{y_0}{k_{\;}}+y_0^2-4=0$的两个不相等的实数根
∴$x_0^2-4≠0$,△>0,${k_1}{k_2}=\frac{y_0^2-4}{x_0^2-4}$…(7分)
∵点R(x0,y0)在椭圆C上,所以$\frac{x_0^2}{12}+\frac{y_0^2}{6}=1$,即$y_0^2=6-\frac{1}{2}x_0^2$
∴${k_1}{k_2}=\frac{{2-\frac{1}{2}x_0^2}}{x_0^2-4}=-\frac{1}{2}$…(8分)
(Ⅲ)OP2+OQ2是定值18.
设直线OP:y=k1x,OQ:y=k2x,${k}_{1}•{k}_{2}=-\frac{1}{2}$,
联立$\left\{\begin{array}{l}y={k_1}x\\ \frac{x^2}{12}+\frac{y^2}{6}=1\end{array}\right.$解得$\left\{\begin{array}{l}x_1^2=\frac{12}{1+2k_1^2}\\ y_1^2=\frac{12k_1^2}{1+2k_1^2}\end{array}\right.$
∴$x_1^2+y_1^2=\frac{{12({1+k_1^2})}}{1+2k_1^2}$
同理,得$x_2^2+y_2^2=\frac{{12({1+k_2^2})}}{1+2k_2^2}$…(10分)
由OP2+OQ2=${{x}_{1}}^{2}+{{y}_{1}}^{2}$+${{x}_{2}}^{2}+{{y}_{2}}^{2}$=$\frac{{12({1+k_1^2})}}{1+2k_1^2}+\frac{{12({1+k_2^2})}}{1+2k_2^2}$,
∴OP2+OQ2=$\frac{{12({1+k_1^2})}}{1+2k_1^2}+\frac{{12({1+k_2^2})}}{1+2k_2^2}$
=$\frac{{12({1+k_1^2})}}{1+2k_1^2}+\frac{{12({1+k_2^2})}}{1+2k_2^2}$=$\frac{{12({1+k_1^2})}}{1+2k_1^2}+\frac{{12({1+k_2^2})}}{1+2k_2^2}$
=$\frac{{12({1+k_1^2})}}{1+2k_1^2}+\frac{{12({1+{{({-\frac{1}{{2{k_1}}}})}^2}})}}{{1+2{{({-\frac{1}{{2{k_1}}}})}^2}}}=\frac{18+36k_1^2}{1+2k_1^2}=18$
综上:OP2+OQ2=18…(12分)
点评 本题考查椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查分类讨论思想、转化思想以及计算能力.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | (-∞,4] | B. | (6,+∞) | C. | (4,6) | D. | [4,6] |
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$或0 | D. | $\sqrt{3}$或0 |
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ | |
| f(x)=Asin(ωx+φ) | 0 | 5 | 0 | -5 | 0 |
(2)将函数y=f(x)的图象向左平移$\frac{π}{6}$个单位长度,得到函数y=g(x)的图象,求y=g(x)的图象离原点O最近的对称中心.
(3)求当$x∈[-\frac{π}{4},\frac{π}{4}]$时,函数y=g(x)的值域.