题目内容
已知数列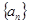 ,
,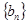 ,
,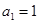 ,
,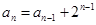 ,
,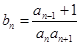 ,
,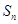 为数列
为数列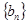 的前
的前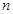 项和,
项和,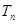 为数列
为数列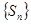 的前
的前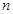 项和.
项和.
(1)求数列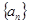 的通项公式;
的通项公式;
(2)求数列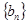 的前
的前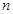 项和
项和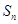 ;
;
(3)求证: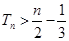 .
.
【答案】
(1)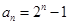 ;(2)
;(2)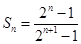 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)解法一是根据数列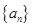 递推式的结构选择累加法求数列
递推式的结构选择累加法求数列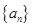 的通项公式;解法二是在数列
的通项公式;解法二是在数列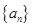 的递推式两边同时除以
的递推式两边同时除以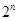 ,然后利用待定系数法求数列
,然后利用待定系数法求数列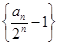 的通项公式,进而求出数列
的通项公式,进而求出数列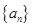 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列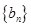 的通项公式,然后根据数列
的通项公式,然后根据数列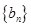 的通项结构,选择裂项相消法求数列
的通项结构,选择裂项相消法求数列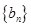 的前
的前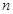 项和
项和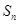 ;(3)对数列
;(3)对数列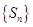 中的项利用放缩法
中的项利用放缩法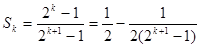
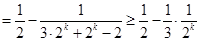 ,然后利用累加法即可证明所要证的不等式.
,然后利用累加法即可证明所要证的不等式.
试题解析:(1)法一: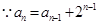
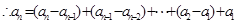 ,
,
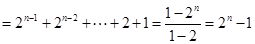
法二: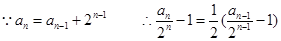
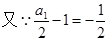

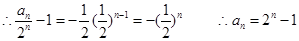
(2)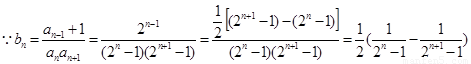
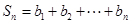
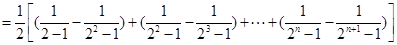
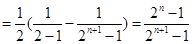
(3)证明: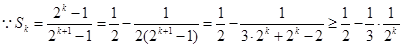 ,
,
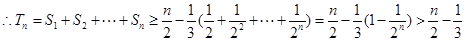 .
.
考点:1.累加法求数列的通项公式;2.待定系数法求数列的通项公式;3.裂项相消法求数列的和;
4.利用放缩法证明数列不等式

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列an=-2n+12,Sn为其前n项和,则Sn取最大值时,n值为( )
| A、7或6 | B、5或6 | C、5 | D、6 |
 (2013•威海二模)已知数列an的通项公式为
(2013•威海二模)已知数列an的通项公式为