题目内容
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x) g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x)
 g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.(1)  (2) [1,+∞)
(2) [1,+∞)
 (2) [1,+∞)
(2) [1,+∞)试题分析:(1)∵|x+1|≥2|x|⇒x2+2x+1≥4x2⇒-
 ≤x≤1,
≤x≤1,∴不等式f(x)≥g(x)的解集为
 .
.(2)若任意x∈R, |x+1|
 2|x|+a恒成立,即任意x∈R, |x+1|-2|x|
2|x|+a恒成立,即任意x∈R, |x+1|-2|x| a恒成立,
a恒成立,令φ(x)=|x+1|-2|x|,则a
 φ(x)max,
φ(x)max,又φ(x)=

当x≥0时,φ(x)≤1;当-1≤x<0时,-2 ≤φ(x)<1;当x<-1时,φ(x)<-2.
综上可得:φ(x)≤1,
∴a
 1,即实数a的取值范围为[1,+∞).
1,即实数a的取值范围为[1,+∞).点评:本题主要考查绝对值不等式的解法,求函数的最小值,函数的恒成立问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




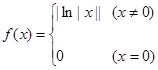 ,则方程
,则方程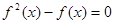 的不相等的实根个数为( )
的不相等的实根个数为( )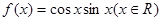 ,给出下列四个命题:
,给出下列四个命题: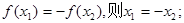 ②
②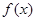 的最小正周期是
的最小正周期是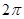 ;
;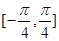 上是增函数; ④
上是增函数; ④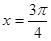 对称;
对称;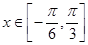 时,
时,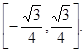 其中正确的命题为
其中正确的命题为  上的偶函数
上的偶函数 ,对任意实数
,对任意实数 都有
都有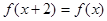 ,当
,当 时,
时,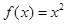 ,若在区间
,若在区间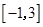 内,函数
内,函数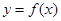 与函数
与函数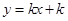 的图象恰有4个交点,则实数
的图象恰有4个交点,则实数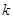 的取值范围是__________.
的取值范围是__________.  有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.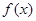 在
在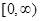 上是增函数,则不等式
上是增函数,则不等式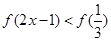 的解集是 .
的解集是 .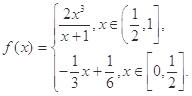 函数
函数 ,若存在
,若存在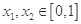 ,使得
,使得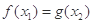 成立,则实数a的取值范围是 .
成立,则实数a的取值范围是 .