题目内容
 高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
 解:(1)根据直方图可以看出②对应的频率是0.025,
解:(1)根据直方图可以看出②对应的频率是0.025,当频率是0.3时,对应的频数是12,按照比例作出①的结果,
用1减去其他的频率得到③的结果,
④处是合计1,
∴①1;②0.025;③0.1;④1
(2)根据频率分布表得到频率分布直方图如图.
(3)利用组中值算得平均数为:
90×0.025+100×0.05+110×0.2+120×0.3+
130×0.275+140×0.1+150×0.05=122.5;
故总体落在[129,155]上的概率为
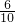 ×0.275+0.1+0.05=0.315.
×0.275+0.1+0.05=0.315.分析:(1)根据直方图可以看出②对应的频率是0.025,当频率是0.3时,对应的频数是12,按照比例作出①的结果,用1减去其他的频率得到③的结果,④是合计,每一个表中这个未知都是1.
(2)根据上一问补充完整的频率分布表,画出频率分步直方图
(3)估计总体落在[129,155]中的概率,利用组中值算得平均数,总体落在[129,155]上的概率为
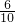 ×0.275+0.1+0.05,得到结果.
×0.275+0.1+0.05,得到结果.点评:本题考查频率分步直方图,考查频率分布表,考查等可能事件的概率,是一个典型的统计问题,注意解题时不要在数字运算上出错.

练习册系列答案
相关题目
 高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:| 分组 | 频数 | 频率 |
| [85,95) | ① | ② |
| [95,105) | 0.050 | |
| [105,115) | 0.200 | |
| [115,125) | 12 | 0.300 |
| [125,135) | 0.275 | |
| [135,145) | 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
(1)根据上面图表,①②③④处的数值分别为多少?
(2)根据题中信息估计总体平均数是多少?
(3)估计总体落在[129,150]中的概率.
| 分组 | 频数 | 频率 |
|
| ① | ② |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(本小题满分12分)高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
|
分组 |
频数 |
频率 |
|
|
① |
② |
|
|
|
0.050 |
|
|
|
0.200 |
|
|
12 |
0.300 |
|
|
|
0.275 |
|
|
4 |
③ |
|
|
|
0.050 |
|
合 计 |
|
④ |
(1)根据上面图表,①、②、③、④处的数值分别是多少?
(2)在坐标系中画出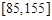 的频率分布直方图;
的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在 中的概率。
中的概率。
 高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:





