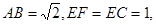题目内容
 在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,G为AD中点.(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求平面BCE与平面ACD所成锐二面角的大小;
(3)求点G到平面BCE的距离.
分析:解法一(空间向量法)(1)建立空间坐标系,设F是线段CE的中点,求出直线BF的方向向量和平面ACD的法向量,根据两个向量垂直可得线面平行;
(2)分别求出平面BCD与平面ACD的法向量,代入向量夹角公式,求出两个向量夹角的余弦值,进而可得二面角的大小
(3)求出BG的方向向量的坐标,进而根据d=|
|,可得点G到平面BCE的距离
解法二(几何法)(1)根据三角形中位线定理及平行四边形的判定和性质,可得BF∥AH,进而由线面平行的判定定理得到BF∥平面ACD
(2)由已知条件可知△ACD即为△BCE在平面ACD上的射影,分别求出两个三角形的面积,代入cosθ=
,可得二面角的大小
(3)连接BG、CG、EG,得三棱锥C-BGE,进而利用等积法,可求出点G到平面BCE的距离.
(2)分别求出平面BCD与平面ACD的法向量,代入向量夹角公式,求出两个向量夹角的余弦值,进而可得二面角的大小
(3)求出BG的方向向量的坐标,进而根据d=|
| ||||
|
|
解法二(几何法)(1)根据三角形中位线定理及平行四边形的判定和性质,可得BF∥AH,进而由线面平行的判定定理得到BF∥平面ACD
(2)由已知条件可知△ACD即为△BCE在平面ACD上的射影,分别求出两个三角形的面积,代入cosθ=
| S△ACD |
| S△BCE |
(3)连接BG、CG、EG,得三棱锥C-BGE,进而利用等积法,可求出点G到平面BCE的距离.
解答: 解:解法一(空间向量法):
解:解法一(空间向量法):
以D点为原点建立如图所示的空间直角坐标系,使得x轴和z轴的正半轴分别经过点A和点E,则各点的坐标为D(0,0,0),B(2,0,1),E(0,0,2),C(1,
,0),
(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为(
,
,1),
∴
=(-
,
,0)
又∵
=(0,0,2)为平面ACD的一个法向量
且
•
=0
∴BF∥平面ACD; …(4分)
(2)设平面BCE的法向量为
=(x,y,z),
则
⊥
,且
⊥
,
由
=(1,-
,1),
=(-1,-
,2)得,
不妨设y=
,则
=(1,
,2)
又∵
=(0,0,2)为平面ACD的一个法向量
∴所求角θ满足cosθ=
=
,
∴平面BCE与平面ACD所成锐二面角的大小为
; …(8分)
(3)由已知G点坐标为(1,0,0),
∴
=(-1,0,-1),
由(2)平面BCE的法向量为
=(1,
,2)
∴所求距离d=|
|=
. …(12分)
解法二:(几何法)
(1)由已知AB⊥平面ACD,DE⊥平面ACD,
∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥ED且FH=ED,
∴FH∥AB且FH=AB,…(2分)
∴四边形ABFH是平行四边形,
∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,
∴BF∥平面ACD;…(4分)
(2)由已知条件可知△ACD即为△BCE在平面ACD上的射影,
设所求的二面角的大小为θ,则cosθ=
,…(6分)
易求得BC=BE=
,CE=2
,
∴S△BCE=
,
而S△ACD=
,
∴cosθ=
=
,
∴θ=
; …(8分)
(3)连接BG、CG、EG,得三棱锥C-BGE,
由ED⊥平面ACD,
∴平面ABED⊥平面ACD,
又CG⊥AD,
∴CG⊥平面ABED,
设G点到平面BCE的距离为h,
则VC-BGE=VG-BCE=
S△BCE•GC=
S△BCE•h,
由S△BCE=
,S△BGE=
,CG=
,
∴h=
即为点G到平面BCE的距离.…(12分)
 解:解法一(空间向量法):
解:解法一(空间向量法):以D点为原点建立如图所示的空间直角坐标系,使得x轴和z轴的正半轴分别经过点A和点E,则各点的坐标为D(0,0,0),B(2,0,1),E(0,0,2),C(1,
| 3 |
(1)点F应是线段CE的中点,下面证明:
设F是线段CE的中点,则点F的坐标为(
| 1 |
| 2 |
| ||
| 2 |
∴
| BF |
| 3 |
| 2 |
| ||
| 2 |
又∵
| DE |
且
| BF |
| DE |
∴BF∥平面ACD; …(4分)
(2)设平面BCE的法向量为
| n |
则
| n |
| CB |
| n |
| CE |
由
| CB |
| 3 |
| CE |
| 3 |
|
不妨设y=
| 3 |
| n |
| 3 |
又∵
| DE |
∴所求角θ满足cosθ=
| ||||
|
|
| ||
| 2 |
∴平面BCE与平面ACD所成锐二面角的大小为
| π |
| 4 |
(3)由已知G点坐标为(1,0,0),
∴
| BG |
由(2)平面BCE的法向量为
| n |
| 3 |
∴所求距离d=|
| ||||
|
|
| 3 |
| 4 |
| 2 |
解法二:(几何法)
(1)由已知AB⊥平面ACD,DE⊥平面ACD,
∴AB∥ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则FH∥ED且FH=ED,
∴FH∥AB且FH=AB,…(2分)
∴四边形ABFH是平行四边形,
∴BF∥AH,
由BF?平面ACD内,AH?平面ACD,
∴BF∥平面ACD;…(4分)
(2)由已知条件可知△ACD即为△BCE在平面ACD上的射影,
设所求的二面角的大小为θ,则cosθ=
| S△ACD |
| S△BCE |
易求得BC=BE=
| 5 |
| 2 |

∴S△BCE=
| 6 |
而S△ACD=
| 3 |
∴cosθ=
| S△ACD |
| S△BCE |
| ||
| 2 |
∴θ=
| π |
| 4 |
(3)连接BG、CG、EG,得三棱锥C-BGE,
由ED⊥平面ACD,
∴平面ABED⊥平面ACD,
又CG⊥AD,
∴CG⊥平面ABED,
设G点到平面BCE的距离为h,
则VC-BGE=VG-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
由S△BCE=
| 6 |
| 3 |
| 2 |
| 3 |
∴h=
| 3 |
| 4 |
| 2 |
点评:本题考查的知识点是二面角的平面角,棱锥的体积,直线与平面平行的判定,其中方法一建立空间坐标系将空间线面关系转化为向量关系,是常用的解题方法,要求熟练掌握.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
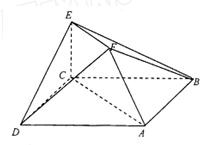 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=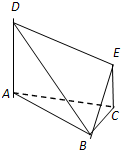 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1. 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,BC⊥AC,EF∥AC,AB=