题目内容
已知函数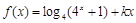
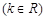 是偶函数.
是偶函数.
(1) 求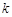 的值;
的值;
(2) 设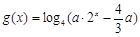 ,若函数
,若函数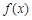 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.
(1)  (2)
(2) 
解析试题分析:解:(1) ∵ 函数
 是偶函数∴
是偶函数∴ 
 恒成立∴
恒成立∴  ,则
,则
(2)  ,函数
,函数 与
与 的图象有且只有一个公共点,即方程
的图象有且只有一个公共点,即方程 只有一个解
只有一个解
由已知得: ∴
∴  方程等价于:
方程等价于: 设
设
 ,则
,则 有一解若
有一解若 ,设
,设 ,∵
,∵ ,∴恰好有一正解∴
,∴恰好有一正解∴  满足题意若
满足题意若 ,即
,即 时,不满足题意若
时,不满足题意若 ,即
,即 时,由
时,由 ,得
,得 或
或 当
当 时,
时, 满足题意当
满足题意当 时,
时, (舍去)综上所述:实数
(舍去)综上所述:实数 的取值范围是
的取值范围是
考点:函数的奇偶性和函数与方程
点评:解决该试题的关键是对于奇偶性定义的准确表示,以及将方程根的问题转换为图像的交点来处理的思想,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
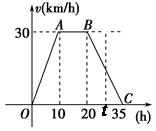
 小时,写出
小时,写出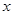 (元/件),可近似看做一次函数
(元/件),可近似看做一次函数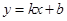 的关系(图象如下图所示).
的关系(图象如下图所示).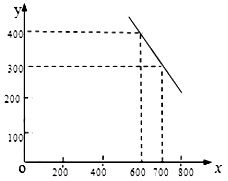
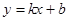 的表达式;
的表达式;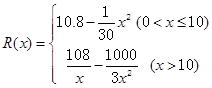
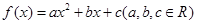 满足下列条件:
满足下列条件: 时,
时,  的最小值为0,且
的最小值为0,且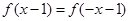 恒成立;
恒成立; 时,
时,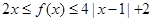 恒成立.
恒成立.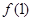 的值;
的值;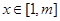 时,就有
时,就有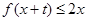 成立
成立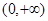 的函数
的函数 ,对任意的
,对任意的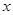 、
、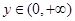 ,都有
,都有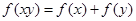 ,且当
,且当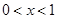 时,
时,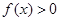 .
.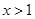 时,
时,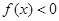 ;
;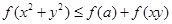 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.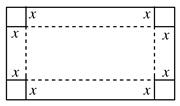
 ,并指出函数
,并指出函数 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.