Question

已知双曲线的方程为,试问:是否存在被点B(1,1)平分的弦?如果存在,求出弦所在的直线方程;如果不存在,请说明理由.

Answer 1

分析:易判断出点B(1,1)在双曲线的外部,不妨假设符合题意的弦存在,那么弦的两个端点应分别在双曲线的左、右两支上,其所在直线的倾斜角也不可能是90°.

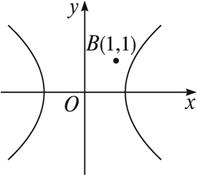
解法一:

如图所示,设被B(1,1)平分的弦所在的直线方程为y=k(x-1)+1,代入双曲线方程为x²-=1,得(k²-2)x²-2k(k-1)x+k²-2k+3=0,

∴Δ=［-2k(k-1)］²-4(k²-2)(k²-2k+3)＞0.

解得k＜,且k≠±,

∴x₁+x₂=.

∵B(1,1)是弦的中点,∴=1.

∴k=2＞.

故不存在被点B(1,1)所平分的弦.

解法二:

设存在被点B平分的弦MN,且M(x₁,y₁),N(x₂,y₂),则x₁+x₂=2,y₁+y₂=2,

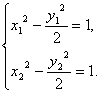
两式相减,得(x₁+x₂)(x₁-x₂)=(y₁+y₂)(y₁-y₂).

∴k_MN=,故直线MN的方程为y-1=2(x-1).

由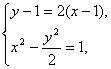消去y,得2x²-4x+3=0,

Δ=(-4)²-4×2×3=-8＜0.

这说明直线MN与双曲线不相交,故被点B平分的弦不存在.

绿色通道：

由本题可以看到,在中点弦问题中,判断点的位置是非常重要的.

如果点B在双曲线的内部,则以该点为中点的弦一定存在.

如果点B在双曲线的外部,则以该点为中点的弦有可能存在.

因此,点B在内部无需检验,点B在外部必须检验.

如上例,以原点为中点的弦存在,以B(1,1)为中点的弦不存在.