题目内容
若f(x)=
在区间(-2,+∞)上是减函数,求a的取值范围.
| ax+3 | x+2 |
分析:利用函数单调递减的定义,设-2<x1<x2,再作差f(x1)-f(x2)后化积,根据f(x)=
在区间(-2,+∞)上是减函数,可求得a的取值范围.
| ax+3 |
| x+2 |
解答:解:对任意的-2<x1<x2
f(x1)-f(x2)=
-
∵-2<x1<x2,则x1+2>0,x2+2>0,x1-x2<0,
由f(x)=
在区间(-2,+∞)上是减函数得f(x1)-f(x2)>0,即
>0,
∴2a-1<0
∴a<
.
f(x1)-f(x2)=
| ax1+1 |
| x1+2 |
| ax2+1 |
| x2+2 |
|
∵-2<x1<x2,则x1+2>0,x2+2>0,x1-x2<0,
由f(x)=
| ax+1 |
| x+2 |
| (2a-1)(x1-x2) |
| (x1+2)(x2+2) |
∴2a-1<0
∴a<
| 1 |
| 2 |
点评:本题考查函数单调性的性质,难点在于思路突破口的选择,着重考查函数单调递减的定义的应用,突出化归思想的考查,属于中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
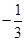 ax
3 + x2 + 2 ( a ≠ 0 ) .
ax
3 + x2 + 2 ( a ≠ 0 ) .