题目内容
已知函数
，
．
⑴用函数单调性的定义证明：函数
在[
]上单调递增；
⑵的定义域和值域都是[]，求常数
的取值范围．
⑴∵
∴
或
、
，当
时，
∵
∴
且
∴
∴
在
上单调递增
⑵∵在上单调递增
∴在上的值域为
∴
且
∴
有两相异的同号根
、
即
∴
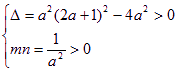
或
．
解析:
单调函数
练习册系列答案
相关题目
解析:
题目内容
已知函数，．
⑴用函数单调性的定义证明：函数在[]上单调递增；
⑵的定义域和值域都是[]，求常数的取值范围．
⑴∵
∴或
、，当时，
∵
∴且
∴
∴在上单调递增
⑵∵在上单调递增
∴在上的值域为
∴且
∴有两相异的同号根、
即
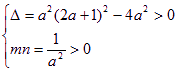
∴或．
单调函数
是定义在
上的奇函数，且
，
的解析式；
.
，请设计一个算法（用自然语言、程序框图两种方式表示）输入x的值，求相应的函数值y．
，请设计一个算法（用自然语言、程序框图两种方式表示）输入x的值，求相应的函数值y．