题目内容
已知公差不为0的等差数列{an}的前3项和S3=9,且a1,a2,a5成等比数列.
(1)求数列{an}的通项公式和前n项和Sn
(2)设Tn为数列{ }的前n项和,若Tn≤λan+1对一切n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对一切n∈N*恒成立,求实数λ的最小值.
解:(1)由S3=9,可得3a1+3d=9即a1+d=3①(2分)
∵a1,a2,a5成等比数列.
∴ ②;
②;
联立①②得a1=1,d=2;…(4分)
故an=2n-1,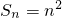 …(6分)
…(6分)
(2)∵ =
= =
=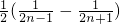 …(8分)
…(8分)
∴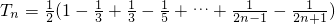 =
= …(10分)
…(10分)
由Tn≤λan+1得:
∴ =
=
令f(n)= ,
,
∵f(n)单调递增,
∴f(n)
即 …(12分)
…(12分)
分析:(1)由等差数列的求和公式可得a1+d=3,由a1,a2,a5成等比数列,可得 ,从而可求a1,d,从而可求
,从而可求a1,d,从而可求
(2)由 =
= =
=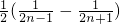 ,利用裂项可求数列的和Tn,然后由Tn≤λan+1得
,利用裂项可求数列的和Tn,然后由Tn≤λan+1得 =
= ,只要求
,只要求 的最大值即可求出λ的范围
的最大值即可求出λ的范围
点评:本题考查的重点是数列的通项与求和,解题的关键是利用等差数列与等比数列的定义,利用裂项法求和.
∵a1,a2,a5成等比数列.
∴
 ②;
②;联立①②得a1=1,d=2;…(4分)
故an=2n-1,
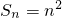 …(6分)
…(6分)(2)∵
 =
= =
=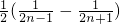 …(8分)
…(8分)∴
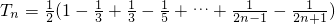 =
= …(10分)
…(10分)由Tn≤λan+1得:

∴
 =
=
令f(n)=
 ,
,∵f(n)单调递增,
∴f(n)

即
 …(12分)
…(12分)分析:(1)由等差数列的求和公式可得a1+d=3,由a1,a2,a5成等比数列,可得
 ,从而可求a1,d,从而可求
,从而可求a1,d,从而可求(2)由
 =
= =
=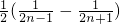 ,利用裂项可求数列的和Tn,然后由Tn≤λan+1得
,利用裂项可求数列的和Tn,然后由Tn≤λan+1得 =
= ,只要求
,只要求 的最大值即可求出λ的范围
的最大值即可求出λ的范围点评:本题考查的重点是数列的通项与求和,解题的关键是利用等差数列与等比数列的定义,利用裂项法求和.

练习册系列答案
相关题目
已知公差不为0的等差数列{an}满足a1,a3,a4成等比关系,Sn为{an}的前n项和,则
的值为( )
| S3-S2 |
| S5-S3 |
| A、2 | ||
| B、3 | ||
C、
| ||
| D、不存在 |