题目内容
设 ,
, 分别是椭圆
分别是椭圆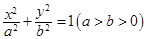 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且 与x轴垂直,直线
与x轴垂直,直线 与C的另一个交点为N.
与C的另一个交点为N.
(1)若直线MN的斜率为 ,求C的离心率;
,求C的离心率;
(2)若直线MN在y轴上的截距为2,且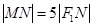 ,求a,b.
,求a,b.
 ,
, 分别是椭圆
分别是椭圆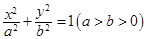 的左右焦点,M是C上一点且
的左右焦点,M是C上一点且 与x轴垂直,直线
与x轴垂直,直线 与C的另一个交点为N.
与C的另一个交点为N.(1)若直线MN的斜率为
 ,求C的离心率;
,求C的离心率;(2)若直线MN在y轴上的截距为2,且
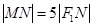 ,求a,b.
,求a,b.(1) ;(2)
;(2) ,
, .
.
 ;(2)
;(2) ,
, .
.试题分析:本题第(1)问,可结合 与x轴垂直,由勾股定理及椭圆定义求出椭圆的离心率;对第(2)问,观察到
与x轴垂直,由勾股定理及椭圆定义求出椭圆的离心率;对第(2)问,观察到 是三角形的中位线,然后结合向量的坐标运算及椭圆方程,可求出a,b.
是三角形的中位线,然后结合向量的坐标运算及椭圆方程,可求出a,b.
试题解析:(1)由题意知, ,所以
,所以 ,由勾股定理可得:
,由勾股定理可得: ,由椭圆定义可得:
,由椭圆定义可得:
 =
= ,解得C的离心率为
,解得C的离心率为 。
。
(2)由题意,原点O为 的中点,
的中点, ∥y轴,所以直线
∥y轴,所以直线 与y轴的交点D(0,2)是线段
与y轴的交点D(0,2)是线段 的中点,故
的中点,故 ,即
,即 ,由
,由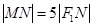 得
得 ,设
,设 ,由题意知
,由题意知 ,则
,则
 ,即
,即 ,代入C的方程得
,代入C的方程得 ,将
,将 及
及 代入
代入 得:
得: ,解得
,解得 ,
, .
.
【易错点】对第(1)问,较容易,大部分同学都能计算出;对第(2)问,一部分同学考虑不到中位线,
容易联立方程组求解而走弯路,并且容易出现计算失误.
 与x轴垂直,由勾股定理及椭圆定义求出椭圆的离心率;对第(2)问,观察到
与x轴垂直,由勾股定理及椭圆定义求出椭圆的离心率;对第(2)问,观察到 是三角形的中位线,然后结合向量的坐标运算及椭圆方程,可求出a,b.
是三角形的中位线,然后结合向量的坐标运算及椭圆方程,可求出a,b.试题解析:(1)由题意知,
 ,所以
,所以 ,由勾股定理可得:
,由勾股定理可得: ,由椭圆定义可得:
,由椭圆定义可得:
 =
= ,解得C的离心率为
,解得C的离心率为 。
。(2)由题意,原点O为
 的中点,
的中点, ∥y轴,所以直线
∥y轴,所以直线 与y轴的交点D(0,2)是线段
与y轴的交点D(0,2)是线段 的中点,故
的中点,故 ,即
,即 ,由
,由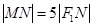 得
得 ,设
,设 ,由题意知
,由题意知 ,则
,则 ,即
,即 ,代入C的方程得
,代入C的方程得 ,将
,将 及
及 代入
代入 得:
得: ,解得
,解得 ,
, .
.【易错点】对第(1)问,较容易,大部分同学都能计算出;对第(2)问,一部分同学考虑不到中位线,
容易联立方程组求解而走弯路,并且容易出现计算失误.

练习册系列答案
相关题目
 (
( )的左焦点为
)的左焦点为 ,离心率为
,离心率为 .
. 上任意一点,过F作TF的垂线交椭圆C于点P,Q.当四边形OPTQ是平行四边形时,求四边形OPTQ的面积.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.当四边形OPTQ是平行四边形时,求四边形OPTQ的面积. 
 的焦点在x轴上,左右顶点分别为
的焦点在x轴上,左右顶点分别为 ,上顶点为B,抛物线
,上顶点为B,抛物线 分别以A,B为焦点,其顶点均为坐标原点O,
分别以A,B为焦点,其顶点均为坐标原点O, 与
与 相交于直线
相交于直线 上一点P.
上一点P. 与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点
与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点 ,求
,求 的最小值.
的最小值.
 +
+ =1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=________.
=1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=________.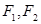 分别是椭圆
分别是椭圆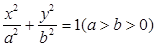 的左右焦点,
的左右焦点,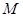 是
是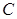 上一点且
上一点且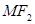 与
与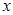 轴垂直,直线
轴垂直,直线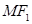 与
与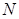 .
.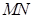 的斜率为
的斜率为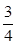 ,求
,求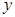 轴上的截距为
轴上的截距为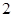 ,且
,且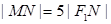 ,求
,求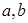 .
.
 的左、右焦点为
的左、右焦点为 、
、 ,离心率为
,离心率为 ,过
,过 交C于A、B两点,若
交C于A、B两点,若 的周长为
的周长为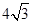 ,则C的方程为
,则C的方程为 B.
B. C.
C. D.
D.
 是平面两定点,点
是平面两定点,点 满足
满足 ,则
,则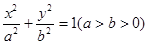 的两顶点为
的两顶点为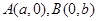 ,且左焦点为F,
,且左焦点为F,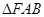 是以角B为直角的直角三角形,则椭圆的离心率
是以角B为直角的直角三角形,则椭圆的离心率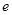 为 ( )
为 ( )



 的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若
的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若 成等比数列,则此椭圆的离心率为________.(离心率
成等比数列,则此椭圆的离心率为________.(离心率 )
)