题目内容
已知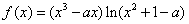 (
(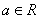 )
)
(Ⅰ)若方程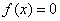 有3个不同的根,求实数
有3个不同的根,求实数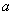 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下,是否存在实数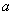 ,使得
,使得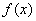 在
在 上恰有两个极值点
上恰有两个极值点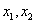 ,且满足
,且满足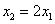 ,若存在,求实数
,若存在,求实数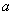 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(Ⅰ)解:由 得:
得: 或
或
可得 或
或 且
且
∵方程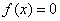 有3个不同的根,
有3个不同的根,
∴方程 有两个不同的根
有两个不同的根
∴
又∵ ,且要保证
,且要保证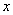 能取到0∴
能取到0∴ 即
即
∴ .
.
(Ⅱ)解:∵
令 ,设
,设
∴
 ∵
∵ ∴
∴ ∴
∴


∵ ∴
∴ ,
, ∴
∴
∴存在 ,使得
,使得 ,另外有
,另外有 ,使得
,使得
假设存在实数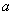 ,使得
,使得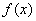 在
在 上恰有两个极值点
上恰有两个极值点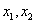 ,且满足
,且满足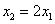
则存在 ,使得
,使得 ,另外有
,另外有 ,即
,即
∴ ,∴
,∴ ,即
,即
即 (*)
(*)
设
∴
∵ ∴
∴
∴ ∴
∴ 在
在 上是增函数
上是增函数
∴
∴方程(*)无解,
即不存在实数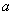 ,使得
,使得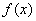 在
在 上恰有两个极值点
上恰有两个极值点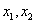 ,且满足
,且满足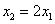

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 的前
的前 项和是
项和是 ,且
,且
 .
. 的通项公式;
的通项公式;
 的正整数
的正整数 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数);以原点
为参数);以原点 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系 ,则曲线
,则曲线 平面ABCD,则点A1的轨迹是( )
平面ABCD,则点A1的轨迹是( )
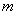 为不小于2的正整数,对任意
为不小于2的正整数,对任意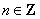 ,若
,若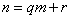 (其中
(其中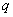 ,
,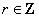 ,且
,且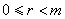 ),则记
),则记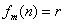 ,如
,如 ,
,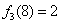 .下列关于该映射
.下列关于该映射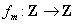 的命题中,正确的是 .
的命题中,正确的是 .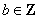 ,则
,则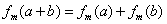
 ,
,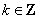 ,且
,且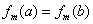 ,则
,则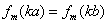
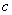 ,
,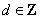 ,且
,且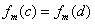 ,则
,则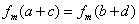
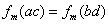


 ,
, 的导函数,即
的导函数,即 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 B.
B.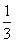 C.
C.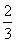 D.
D.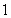
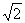 ,(1,2)
,(1,2)